I.3. Расчет интерференционной картины от двух когерентных источников. Расчет интерференционной картины в тонкой пленке
Материал презентаций по физике / Часть 3 / Лекция 3 / Лекция 3
9
Лекция 3
Волновая оптика
Вопросы
1. Расчет интерференционной картины от двух источников.
2. Интерференция света в тонких пленках.
3. Кольца Ньютона.
4. Применение интерференции света
1. Расчет интерференционной картины от двух источников
В качестве примера рассмотрим метод Юнга. Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие равноудаленные щели S1 и S2, параллельные щели S. Таким образом, щели S1 и S2 играют роль когерентных источников. Интерференционная картина (область ВС) наблюдается на экране Э, расположенном на некотором расстоянии параллельно S1 и S2. Юнгу принадлежит первое наблюдение явления интерференции.
Интенсивность в любой точке М экрана, лежащей на расстоянии х от точки 0, определяется разностью хода
Δ = L2 L1 (1)
;

; 
;
Так как l >> d, то L2 + L1 2l и
. (2)
Условие максимума Δ = mλ; (m = 0, ±1, ±2, ...) 

. (3)
Условие минимума 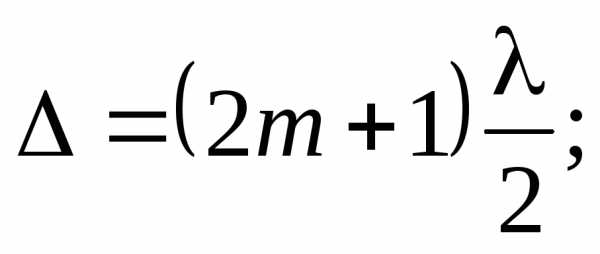 (m = 0, ±1, ±2, ...)
(m = 0, ±1, ±2, ...) 

. (4)
Шириной интерференционной полосы называется расстояние между двумя соседними максимумами (или минимумами)
, (5)
ширина интерференционной полосы 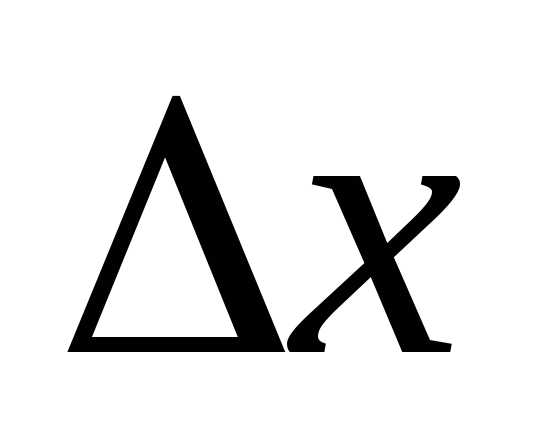 не зависит от порядка интерференцииm и является постоянной. Главный максимум интерференции при m = 0 в центре, от него максимумы первого (m = 1), второго (m = 2) и т. д. порядков.
не зависит от порядка интерференцииm и является постоянной. Главный максимум интерференции при m = 0 в центре, от него максимумы первого (m = 1), второго (m = 2) и т. д. порядков.
Для видимого света 10-7 м , 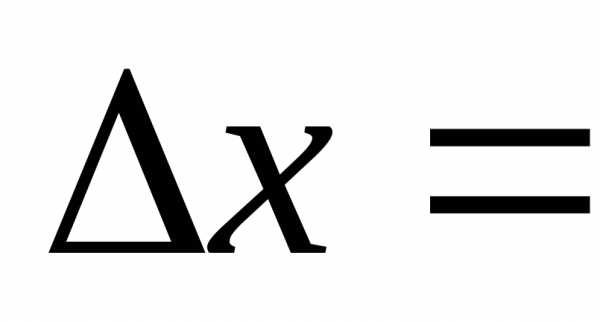 0,1 мм = 10-4 м (разрешающая способность глаза) интерференция наблюдается при l/d = x/ > 103.
0,1 мм = 10-4 м (разрешающая способность глаза) интерференция наблюдается при l/d = x/ > 103.
При использовании белого света с набором длин волн от фиолетовой ( = 0,39 мкм) до красной ( = 0,75 мкм) границ спектра при m = 0 максимумы всех волн совпадают, далее при m = 1, 2, … спектрально окрашенные полосы, ближе к белой фиолетовый, дальше красный.
2. Интерференция света в тонких пленках

Интерференцию света можно наблюдать не только в лабораторных условиях с помощью специальных установок и приборов, но и в естественных условиях. Так, легко наблюдать радужную окраску мыльных пленок, тонких пленок нефти и минерального масла на поверхности воды, оксидных пленок на поверхности закаленных стальных деталей (цвета побежалости). Все эти явления обусловлены интерференцией света в тонких прозрачных пленках, возникающей в результате наложения когерентных волн, возникающих при отражении от верхней и нижней поверхностей пленки.
Оптическая разность хода лучей 1 и 2
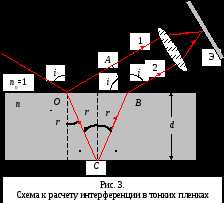
где п – показатель преломления пленки; n0 – показатель преломления воздуха, n0 = 1; λ0/2 – длина полуволны, потерянной при отражении луча 1 в точке О от границы раздела с оптически более плотной средой (n>n0,).
;
;
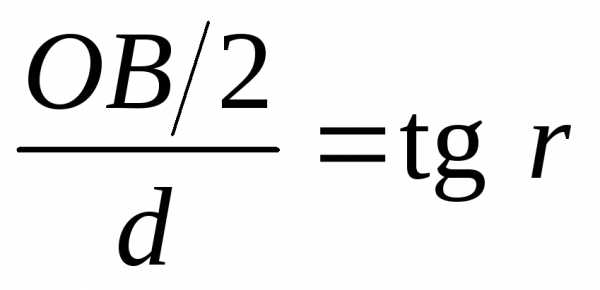


 ;
;
.
. (7)
Условие максимума
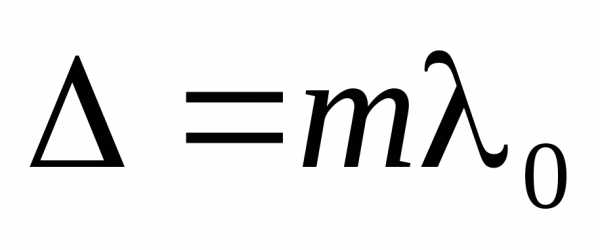 : (8)
: (8)
Условие минимума
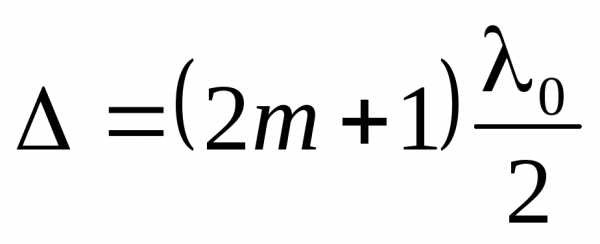 : (9)
: (9)
При освещении пленки белым светом она окрашивается в какой-либо определенный цвет, длина волны которого удовлетворяет максимуму интерференции. Следовательно, по цвету пленки можно оценивать её толщину.
Условия (8), (9) зависят при постоянных значениях n, 0 от угла падения i и толщины пленки d, в зависимости от этого различают полосы равного наклона и полосы равной толщины.
Полосами равного наклона называют интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами.
Полосами равной толщины называют интерференционные полосы, возникающие в результате наложения лучей, падающих на пластинку переменной толщины от мест одинаковой толщины.
3. Кольца Ньютона
Кольца Ньютона классический пример полос равной толщины.
В отраженном свете оптическая разность хода (с учетом потери полуволны λ0/2 при отражении от плоскопараллельной пластинки):
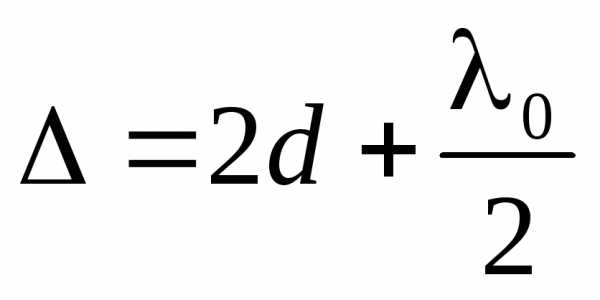 , (10)
, (10)
где d – ширина зазора.
R2 = r2 + (R – d)2 
 (d << R)
(d << R) 
 .
.
. (11)
Условие максимума  радиус светлого кольца
радиус светлого кольца
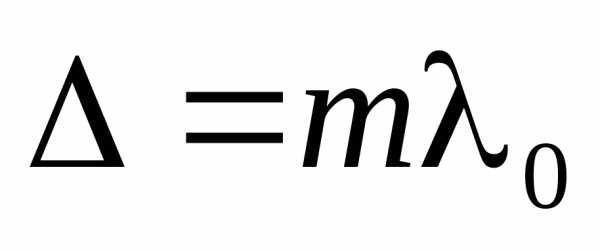 :
: 
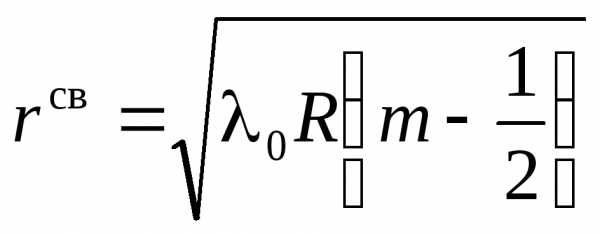 (12)
(12)
Условие минимума  радиус темного кольца
радиус темного кольца
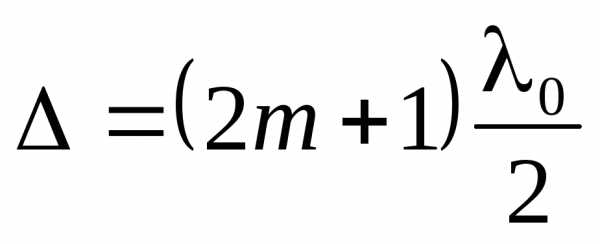 :
:  (13)
(13)
Система светлых и темных полос получается только при освещении монохроматическим светом. В белом свете интерференционная картина изменяется, каждая светлая полоса превращается в спектр.
Кольца Ньютона можно наблюдать и в проходящем свете. При этом максимумы интерференции в отраженном свете соответствуют минимумам в проходящем и наоборот.
Измеряя радиусы колец Ньютона, можно определить λ0 (зная радиус кривизны линзы R ) или R (зная λ0 ).
4. Применение интерференции света
4.1. Интерференционная спектроскопия измерение длин волн.
4.2. Улучшение качества оптических приборов («просветленная оптика») и получение высокоотражающих покрытий.
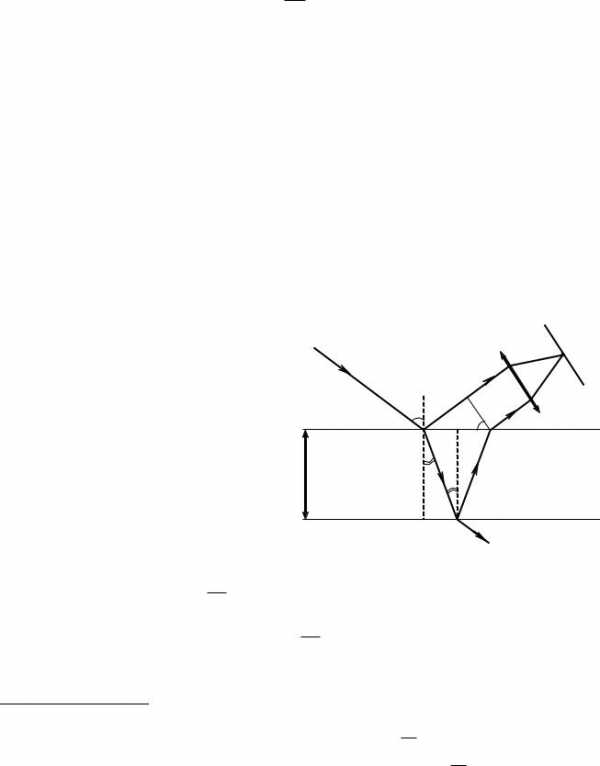
Прохождение света через каждую преломляющую поверхность линзы, например, через границу стекло - воздух, сопровождается отражением ~ 4 % падающего потока (при показателе преломления стекла n = 1,5). Так как современные объективы содержат большое количество линз, потери светового потока из-за отражений велики. В результате интенсивность прошедшего света ослабляется, и светосила оптического прибора уменьшается. Кроме того, отражение от поверхностей линз приводит к возникновению бликов, что, например, в военной технике, демаскирует местонахождение прибора. Для устранения указанных недостатков осуществляют так называемое просветление оптики. С этой целью на поверхности линз наносят тонкие пленки с показателем преломления, меньшим показателя преломления материала линз (1< n < nст). При отражении света от границ раздела - воздух - пленка и пленка - стекло возникает интерференция когерентных лучей 1 и 2 .
Толщину пленки d и показатели преломления стекла nст и пленки ппл подбирают так, чтобы при интерференции в отраженном свете лучи 1 и 2 гасили друг друга. Для этого их оптическая разность хода должна удовлетворять условию
, (14)
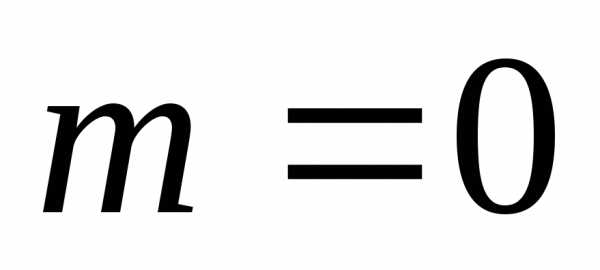 ;
; 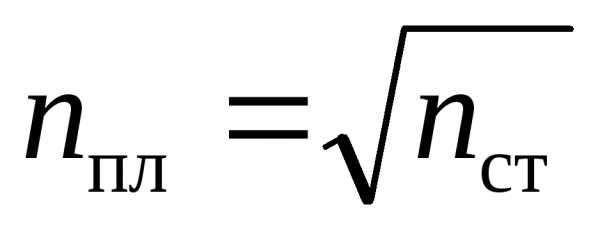

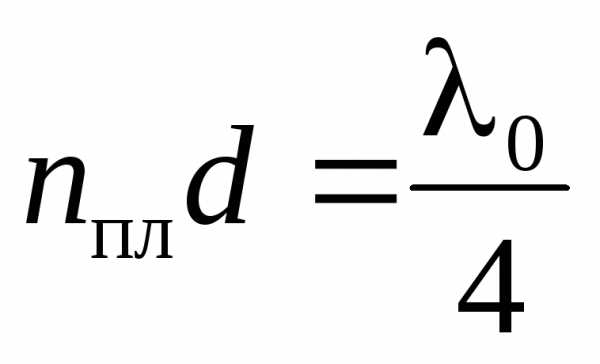

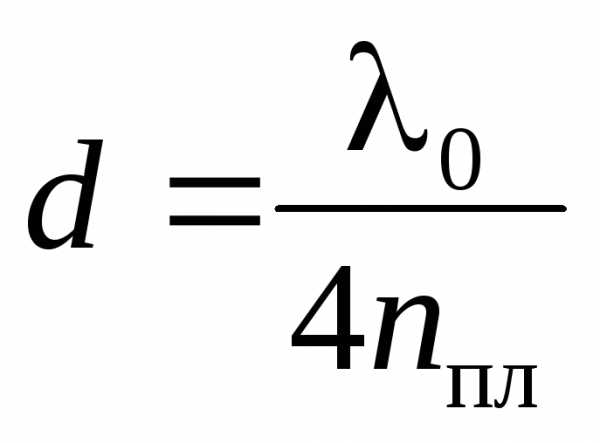 . (15)
. (15)
Так как добиться одновременного гашения всех длин волн спектра невозможно, то это обычно делается для зеленого цвета (λ0 = 550 нм), к которому человеческий глаз наиболее чувствителен (в спектре излучения Солнца эти лучи имеют наибольшую интенсивность).
В отраженном свете объективы с просветленной оптикой кажутся окрашенными в красно-фиолетовый цвет. Для улучшения характеристик просветляющего покрытия его делают из нескольких слоев, что «просветляет» оптические стекла более равномерно по всему спектру.
4.3. Интерферометр прибор, служащий для точного (прецизионного) измерения длин, углов, показателей преломления и плотности прозрачных сред и т.д.
Интерференционная картина очень чувствительна к разности хода интерферирующих волн: ничтожно малое изменение разности хода вызывает заметное смещение интерференционных полос на экране.
Все интерферометры основаны на одном и том же принципе - делении одного луча на два когерентных - и различаются лишь конструктивно.
Интерферометр Майкельсона.
S источник света;
Р1 полупрозрачная пластинка;
Р2 прозрачная пластина;
М1, М2 зеркала.
Лучи 1′ и 2′ когерентны, следовательно, наблюдается интерференция, результат которой будет зависеть от оптической разности хода луча 1 от точки 0 до зеркала М1 и луча 2 от точки 0 до зеркала М2. По изменению интерференционной картины можно судить о малом перемещении одного из зеркал. Поэтому интерферометр Майкельсона применяется для точных (~ 10-7 м) измерений длин.
Самый известный эксперимент, выполненный Майкельсоном (совместно с Морли) в 1887 г., ставил целью обнаружить зависимость скорости света от скорости движения инерциальной системы координат. В результате было установлено, что скорость света одинакова во всех инерциальных системах, что послужило экспериментальным обоснованием для создания специальной теории относительности Эйнштейна.
Интерференционный дилатометр прибор для изменения длины тела при нагревании.
Советский физик академик В.П. Линник использовал принцип действия интерферометра Майкельсона для создания микроинтерферометра (комбинация интерферометра и микроскопа), служащего для контроля чистоты обработки поверхности металлических изделий. Таким образом, интерферометр Линника является прибором, предназначенным для визуальной оценки, измерения и фотографирования высот микронеровностей поверхности вплоть до 14-го класса чистоты поверхности.
Другим чувствительным оптическим прибором является рефрактометр интерферометр Рэлея. Он применяется для определения незначительных изменений показателя преломления прозрачных сред в зависимости от давления, температуры, примесей, концентрации раствора и т.д. Интерферометр Рэлея позволяет измерять изменение показателя преломления c очень высокой точностью Δn ~ 10 -6 .
studfiles.net
I.3. Расчет интерференционной картины от двух когерентных источников

быть выражено через разность хода: если оптическая разность хода двух когерентных волн равна четному числу полуволн в вакууме
= ±2k λ20 , (I.7)
то в данной точке вóлны усиливают друг друга, наблюдается максимум интенсивности света.
Условие интерференционных минимумов. Если разность фаз равна нечетному числу π, т.е.
δ = ± (2k + 1)π,
то в данной точке пространства происходит ослабление колебаний. С учетом формулы (I.6) условие минимумов интерференции может быть выражено через разность хода: если оптическая разность хода двух когерентных волн равна нечетному числу полуволн в вакууме
= ± (2k + 1) | λ0 | , | (I.8) | |
2 | ||||
|
|
|
то в данной точке вóлны гасят друг друга, наблюдается минимум интенсивности света.
При наблюдении интерференции в монохроматическом свете интерференционная картина представляет собой чередование светлых и темных участков. Интерференционная картина в белом свете приобретает радужную окраску.
Рассмотрим два когерентных источника света S1 иS2, расстояние между которыми равноd (рис. I.8). В поле интерференции внесем экран, на котором бу-
дет наблюдаться интерференцион- |
|
|
| x |
ная картина. Расстояние от источ- |
|
|
| |
|
|
| P | |
ников до экрана равно l. Пусть на | S1 | r1 |
| x |
экране в некоторой точке P с коор- | r2 | d/2 | ||
динатой x наблюдается интерфе- | d |
| ||
ренционный максимум или мини- |
| d/2 | O | |
|
| |||
мум. Квадраты расстояний от ис- | S2 |
|
| |
l |
|
| ||
точников S1 иS2 до точкиР соответ- |
|
|
| |
|
|
|
| |
ственно равны |
| Рис. I.8 |
|
|
r12 =l2 +( x −d )2 , | (I.9) | |||
|
| 2 |
|
|
r22 =l2 +( x + | d )2 . |
| (I.10) | |
|
| 2 |
|
|
Вычтем уравнение (I.9) из уравнения (I.10): |
|
|
| |
r22 −r12 =( x + | d )2 − | ( x − | d )2 . |
|
| 2 |
| 2 |
|
Выполнив преобразования, получим |
|
|
|
|
(r2 –r1)(r2 +r1) = 2xd. |
| |||
Интерференционная картина будет наблюдаться, если d <<l иx <<l. Тогда | ||||
r2 +r1 ≈ 2l, т.е. |
|
|
|
|
2l(r2 –r1) = 2xd, |
|
| ||
откуда геометрическая разность хода | r =r2 –r1 равна |
| ||
r =xdl .
Умножим правую и левую часть полученного уравнения на n (показатель преломления среды, в которой распространяются когерентные волны):
n r = | n | xd |
l . | ||
Слева имеем оптическую разность хода |
| , следовательно |
=n xdl .
Всоответствии с условием интерференционного максимума (I.7)
n xd | = ± kλ . |
| ||
l |
|
|
|
|
Так как λ/n = λ0, то для координат интерференционных максимумов имеем |
| |||
x = | ± k | lλ0 | . | (I.11) |
| ||||
max |
| d |
| |
|
|
|
| |
Аналогично, в соответствии с условием (I.8), получим формулу для координат интерференционных минимумов:
xmin | = ± (k +1 ) | lλ0 | . | (I.12) |
| ||||
| 2 | d |
| |
Ширина интерференционной полосы | x есть расстояние между соседними мак- | |||
симумами или соседними минимумами. Величину | x можно определить, если | |||
взять разность координат соседних максимумов (или соседних минимумов) | ||||||||
x =хk+1 –xk. Тогда ширина интерференционной полосы равна |
| |||||||
|
|
| x = | lλ0. |
|
|
| (I.13) |
|
|
|
| d |
|
|
|
|
| I.4. Интерференция света в тонких пленках |
| ||||||
Пусть на тонкую пленку (или на тонкую прозрачную пластинку) падает луч | ||||||||
монохроматического света (рис. I.9) под некоторым углом α. Падающий луч в | ||||||||
точке падения А частично отражается и частично преломляется в пленке. Луч, | ||||||||
отраженный от нижней поверхности пленки в точке В, выходит из пленки в | ||||||||
точке С. Волновая поверхностьCD перпендикулярна отраженным лучам1 и2. | ||||||||
Эти лучи являются когерентными, поскольку образованы из одной световой | ||||||||
волны. Лучи 1 и2 фокусируются линзойЛ на экранеЭ в точкеP, в которой | ||||||||
происходит интерференция. В результате интерференции в точке Р будет на- | ||||||||
блюдаться свет (если выполняется |
|
|
|
|
| |||
условие интерференционных мак- |
|
|
| Л | P | |||
симумов) или темнота (если вы- |
|
|
| |||||
полняется условие интерференци- |
|
|
| 1 |
| |||
онных минимумов). Результат ин- |
|
| α | D | Э | |||
|
| α C | ||||||
терференции | можно | наблюдать |
|
|
| |||
|
| A |
| |||||
|
|
|
| |||||
глазом. Поскольку лучи 1 и2 па- |
|
|
|
| ||||
d | n | β |
|
| ||||
раллельны друг другу, глаз должен | β |
| ||||||
|
| |||||||
быть аккомодирован в бесконеч- |
|
|
|
|
| |||
ность. Оптическая разность | хода |
|
|
| B |
| ||
лучей 1 и2 равна |
|
|
|
| Рис. I.9 |
| ||
= n(AB +BC) –AD –λ0 |
|
|
|
| ||||
, |
|
|
|
|
| |||
|
| 2 |
|
|
|
|
|
|
где n – показатель преломления пленки,λ0 | – потеря полуволны при отражении | |||||||
|
|
|
| 2 |
|
|
|
|
луча 1 от оптически более плотной среды1. Из рис. I.9 видно, что |
| |||||||
1 При отражении световой волны от оптически более плотной среды фаза колебаний меняется на π радиан, что соответствует изменению разности хода наλ20 . При этом в выражении
для оптической длины пути следует добавить (или вычесть) слагаемое λ20 .
AB | = BC = |
|
| d |
|
| ; | AC = 2dtgβ; |
| AD =ACsinα = 2dtgβsinα. | ||||||||||||||||
| cosβ |
| ||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
| λ0 |
|
|
|
|
|
|
|
| 2dsinβsinα |
| λ0 | ||||
| n | 2d |
|
| − 2dtgβsinα − |
|
| n | 2d |
| ||||||||||||||||
= |
| 2 |
|
| = |
|
| − | cosβ |
|
| − | 2 . | |||||||||||||
cosβ |
|
| cosβ |
|
| |||||||||||||||||||||
Поскольку sinα = nsinβ, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
| 2d |
|
|
| 2 |
| λ0 |
|
|
|
|
|
|
| 2 | ц |
| λ0 |
| ||||
|
|
|
|
|
|
| 2dnsinβ |
|
|
|
|
| ж1 −sin β |
|
| |||||||||||
| = n |
|
|
|
| − |
|
| − |
|
|
| = |
| 2dnз |
|
| ч | − |
|
| . | ||||
| cosβ |
| cosβ |
| 2 |
|
|
| cosβ |
| 2 | |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| и | ш |
|
|
| ||||||||||
Следовательно, оптическая разность хода лучей 1 и2 равна |
|
|
|
| ||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| = 2dncosβ – | λ0 | , |
|
|
|
| (I.14) | |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| |||
где d – толщина пленки, β – угол преломления. Учитывая, что cosβ =1 − sin2β ,
и выражая по закону преломления sinβ = sinαn , получим еще одну формулу для оптической разности хода лучей1 и2:
|
|
|
|
|
| λ |
|
|
|
= 2d n | 2 | − | 2 | − | 0 |
|
| ||
| sinα |
| . | (I.15) | |||||
| 2 | ||||||||
|
|
|
|
|
|
|
| ||
Полосы равного наклона. На тонкую пленку толщинойd (d = const) падает рассеянный монохроматический свет (λ0 = const). В рассеянном свете имеются лучи различных направлений, поэтому углы падения лучей принимают значения от 0 до π/2. Покажем на чертеже (рис. I.10) лучи, которые падают под некоторым углом α и лежат в плоскости чертежа. Лучи, отраженные от верхней и от нижней поверхности пленки фокусируются собирающей линзойЛ, в фокальной плоскости которой расположен экранЭ. Освещенность в точкеР на экране будет определяться оптической разностью хода интерферирующих лучей. Лучи, которые идут в другой плоскости, но падают под тем же углом α, соберутся линзой в других точках экрана на таком же расстоянии от точкиО, что и точкаР. Таким образом, лучи рассеянного света, падающие под углом α, создадут на экране одну и ту же освещенность (по окружности или по дуге окружности с центром в точкеО).
Лучи, падающие под другим углом α′, создадут на экране совокупность точек с другой освещенностью (т.к. оптическая разность хода интерферирующих лучей изменится).
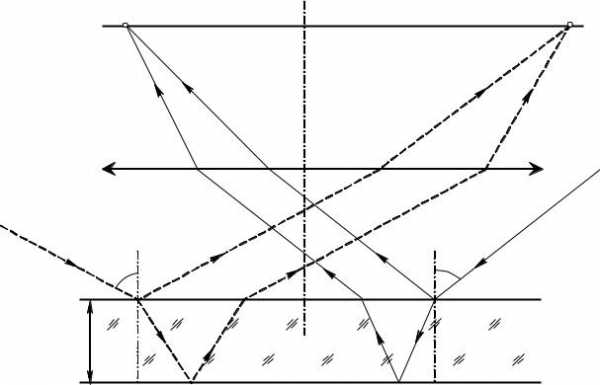
Л
d
Рис. I.10
Образуется окружность другого радиуса и другой освещенности. Для всей совокупности лучей на экране возникает система чередующихся светлых и темных круговых полос с центром в точке О. Интерференционная картина в этом случае называетсяполосами равного наклона, поскольку каждая полоса образована лучами, падающими на пленку под одинаковыми углами. В случае белого света интерференционная картина приобретает радужную окраску.
Полосы равной толщины наблюдаются при интерференции света в случае отражения лучей от пленок переменной толщины или в клинообразных пластинках. Рассмотрим падение лучей монохроматического света на поверхность клинообразной пластинки под равными углами α (рис. I.11). Падающие лучи частично отражаются от верхней поверхности клина, частично преломляются в клине и отражаются от его нижней поверхности, образуются когерентные лучи (лучи1,2 и1′,2′ на рис. I.11). Разность хода лучей, интерферирующих в различных по толщине местах пленки, неодинакова. Эта разность остается постоянной вдоль линии, параллельной ребру клина, и убывает от основания к ребру. Отраженные лучи могут быть сфокусированы при помощи линзы, тогда на
13
studfiles.net
1. Метод Юнга.
1. Электромагнитная природа света. Сложение колебаний, понятие о когерентности. Интерференция световых волн. Расчет интерференционной картины от двух источников. Пространственная и временная когерентность. Оптическая длина пути. Способы получения интерференционных картин . Интерференция в тонких пленках. Полосы равной толщины и равного наклона. Кольца Ньютона. Многолучевая интерференция. Практическое применение явления интерференции. Интерферометры.
Электромагнитная природа света.
Т.к. свет представляет собой электромагнитные волны, то в основе волновой оптики лежат уравнения Максвелла и вытекающие из них соотношения для электромагнитных волн. Согласно электромагнитной теории Максвелла , где с и v соответственно скорости распространения света в среде с диэлектрической проницаемостью и магнитной проницаемостью μ и в вакууме. Это соотношение связывает оптические, электрические и магнитные постоянные вещ-ва. По Максвеллу, и μ -- величины, не зависящие от длины волны света, поэтому электромагнитная теория не могла объяснить явление дисперсии (зависимость показателя преломления от длины волны). Значения показателя преломления характеризуют оптическую плотность среды (оптически более и менее плотные среды). Длина световой волны в среде с показателем n связана с длиной волны в вакууме: .
Сложение колебаний, понятие о когерентности.
В классической волновой оптике рассматриваются среды, линейные по своим оптическим св-вам, т.е такие, диэлектрическая и магнитная проницаемость которых н.з. от интенсивности света. Поэтому в волновой оптике справедлив принцип суперпозиции волн. Явления, наблюдающиеся при распространении света в оптически нелинейных средах, исследуются в нелинейной оптике. Нелинейные оптические эффекты становятся существенными при очень больших интенсивностях света, излучаемого мощными лазерами. Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления:
. Амплитуда результирующего колебания в данной точке будет: где. Если разность фаз δ возбуждаемых волнами колебаний остается постоянной во времени, то волны наз-ся когерентными.
Интерференция световых волн.
Явление интерференции света состоит в отсутствии суммирования интенсивностей
световых волн при их наложении, т.е. во взаимном усилении этих волн в одних точках пространства и ослаблении – в других. Необходимым условием интерференции волн является их когерентность. Этому условию удовлетворяют монохроматические волны одинаковой частоты (неограниченные в пространстве волны одной определенной и строго постоянной частоты). Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда
некогерентны (например, две лампочки). Однако из-за поперечности электромагнитных волн условие их когерентности еще не достаточны для получения интерференционной картины. Необходимо, кроме того, чтобы колебания
векторов Е электромагнитных полей интерферирующих волн совершались вдоль
одного и того же или близких направлений. Продолжительность процесса излучения света атомом t~10-8 с. За этот промежуток времени возбужденный атом, растратив свою избыточную энергию на излучение, возвращается в
нормальное (невозбужденное) состояние и излучение им света прекращается. Затем, спустя некоторый промежуток времени атом может вновь возбудиться и начать излучать свет. Такое прерывистое излучение света атомами в виде
отдельных кратковременных импульсов – цугов волн – характерно для любого источника света независимо от специфических особенностей тех процессов, которые происходят в источнике и вызывают возбуждение его атома.
Расчет интерференционной картины от двух источников.
Расчет интерференционной картины для двух источников можно провести используя две узкие параллельные щели, расположенные достаточно близко друг к другу.
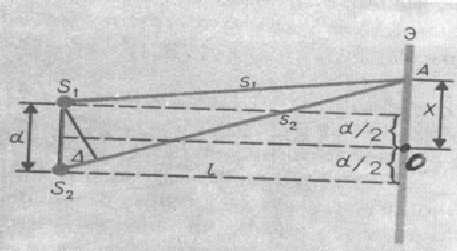
Щели инаходятся на расстоянииd друг от друга и являются когерентными источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей. Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода (разностью оптических длин проходимых волнами путей).
Из рисунка имеем: откуда или . Из условия l>>d следует, что поэтому . Подставив найденное значение Δ в условия интерференционного максимума и минимума: и
, получим, что максимумы интенсивности будут наблюдаться при , а минимумы – при. Расстояние между двумя соседними максимумами (или минимумами) называемое шириной интерференционной полосы равно:. Δx не зависит от порядка интерференции (величины m) и является постоянной для . Δx обратно пропорционально d, след. при большом расстоянии между источниками, например, d ≈ l , отдельные полосы становятся неразличимыми. Из двух предпоследних формул следует так же, что интерференционная картина , создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m=0, проходит через точку О. Вверх и вниз от него, на равных расстояниях располагаются максимумы (минимумы) первого (m=1) и других порядков. Описанная картина справедлива только лишь при освещении монохроматическим светом. Если использовать белый свет, то интерференционные максимумы для каждой длины волны будут смещены друг относительно друга и иметь вид радужных полос. Только для m=0 максимумы всех длин волн совпадают, а в середине экрана будет наблюдаться белая полоса.
Пространственная и временная когерентность.
Любой монохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга называется временем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, . Если волна распространяется в однородной среде, то фаза колебаний в определенной точке пространства сохраняется только в течении времени когерентности. За это время волна распространяется в вакууме на расстояние , называемое длиной когерентности. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света. Чем ближе волна к монохроматической, тем меньше ширина спектра ее частот и больше ее время когерентности, а следовательно и длина когерентности. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временной когерентностью. Наряду с временной когерентностью, для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Два источника, размеры которых позволяют (при необходимой степени монохроматичности света) наблюдать интерференцию, называются пространственно когерентными.
Оптическая длина пути.
Пусть разделение на две когерентные волны происходит в одной определенной точке О. До точки М, в которой наблюдается интерференционная картина, одна волна в результате преломления прошла путь, вторая – в среде– путь. Если в точке О фаза колебаний равнаωt , то в точке М первая волна возбудит колебание вторая волна – колебание где –фазовая скорость первой и второй волны. Произведение геометрической длины S пути световой волны в данной среде на показатель преломления этой среды называется оптической длиной волны L, a – разность оптических длин проходимых путей – оптическая разность хода. Если оптическая разность хода равна целому числу волн в вакууме , то и колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно, это максимум. Если оптическая разность хода тои колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Следовательно мин..
Способы получения интерференционных картин.
Для осуществления интерференции света необходимо получить когерентные световые пучки, для чего применяются различные приемы. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел.
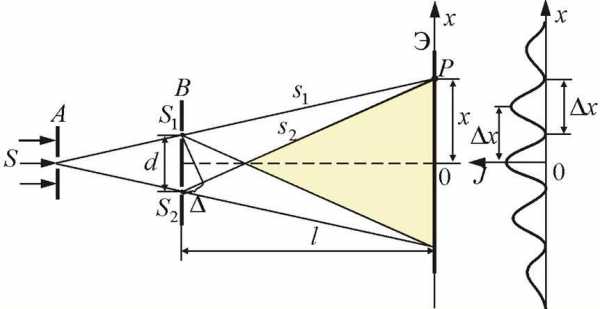
Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие равноудаленные щели и, параллельные щели S. Таким образом, щелиииграют роль когерентных источников. Интерференционная картина (область ВС) наблюдается на экране Э, расположенном на некотором расстоянии параллельнои.
2.Зеркала Френеля.
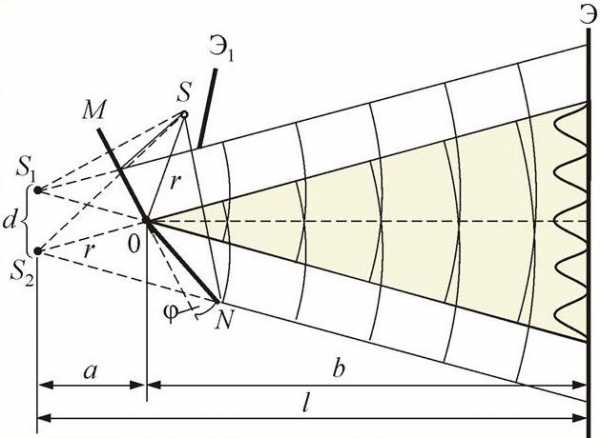
Свет от источника S падает расходящимся пучком на два плоских зеркала и, расположенных относительно друг друга под углом, лишь немного отличающимся от(уголмал). Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источникови, являющихся мнимыми изображениямиS в зеркалах. Мнимые источники ивзаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рисунке это раскрашенная область). Интерференционная картина наблюдается на экране на экране Э, защищенного от прямого попадания света заслонкой З
3. Бипризма Френеля.
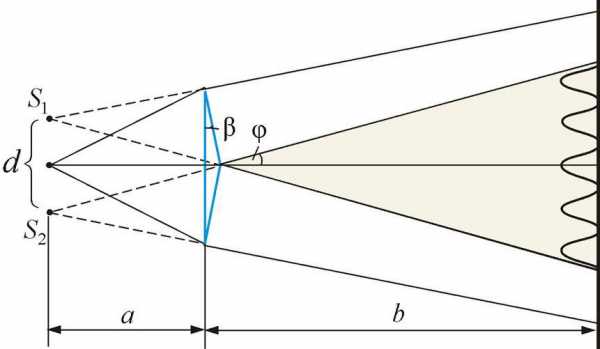
Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников и, являющихся когерентными. Таким образом, на поверхности экрана (в области выполненной в цвете) происходит наложение когерентных пучков и наблюдается интерференция.
Интерференция в тонких пленках.
В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри и т.д.) возникающее в р- тате интерференции света, отраженного двумя поверхностями пленки. Пусть на плоскопараллельную прозрачную пленку с показателем преломления n и толщиной d под углом i падает плоская монохроматическая волна (для простоты рассм. один луч).
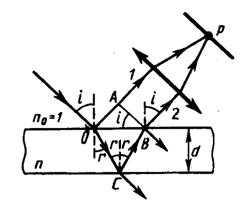
На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, и частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (), и частично отразится и пойдет к точке В. Здесь он опять частично отразится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом i. Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы и дадут интерференционную картину, которая определится оптической разностью хода между интерферирующими лучами. Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки О до плоскости АВ:где показатель преломления окружающей среды принят равным 1, аобусловлен потерей полуволны при отражении света от границы раздела. Если, то потеря полуволны произойдет в точке О (C) ибудет иметь знак минус (плюс).
Полосы равной толщины и равного наклона.
Полосы равного наклона (интерференция от плоскопараллельной пластинки).
Интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами . Для данных ,d, n каждому наклону i лучей соответствует своя интерференционная полоса.
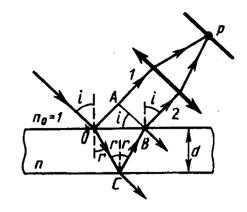
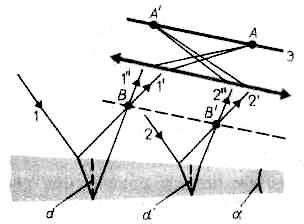
Интерференционные полосы, возникающие в результате наложения лучей падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона. Лучи 1’ и 1”, отразившиеся от верхней и нижней граней пластинки, параллельные друг другу, так как пластинка плоскопараллельна. Следовательно, интерферирующие лучи 1’ и 1” «пересекаются» только в бесконечности. Для их наблюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1’ и 1” соберутся в фокусе F линзы , в эту же точку придут и другие лучи, параллельные лучу 1, в результате чего увеличивается общая интенсивность. Лучи 3, наклоненные под другим углом , соберутся в другой точке фокальной плоскости линзы. Если оптическая ось линзы перпендикулярна поверхности пластинки, полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы.
studfiles.net
6) Расчет интерференционной картины от двух когерентных источников. Оптическая длина пути.
Рассмотрим более подробно основные свойства интерференционной картины, создаваемой двумя источниками электромагнитных волн одинаковой интенсивности и наблюдаемой на плоском экране, расположенным на расстоянии l от плоскости расположения от источников. В качестве таких источников могут мыслиться, например две бесконечно-узкие, параллельные друг - другу щели или два отверстия бесконечно малого диаметра, расстояние между которыми d<<l , прорезанные в плоском непрозрачном экране. Пусть источники электромагнитных волн располагаются в однородной среде с показателем преломления.
Область, в которой волны источников перекрываются, называется полем интерференции. В поле интерференции имеются места, где волны источников будут складываться в фазе. В этих местах будут отмечаться максимумы интенсивности электромагнитного поля. Там же, где волны будут складываться в противофазе - минимальная интенсивность . Если в поле интерференции поместить непрозрачный экран, то будет наблюдается чередование светлых и тёмных полос (рис. 4.3a), представляющие собой интерференционную картину. 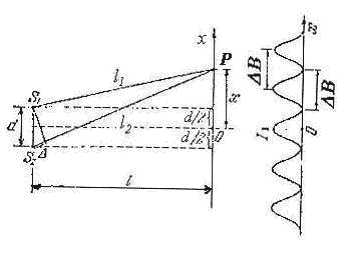
Расчет интерференционной картины от двух когерентных источников. Оптическая длина пути.
l1 и l2 расстояния, проходимые волнами соответственно от первого и второго источников до точки наблюдения.
Из (l1 + l2)~2 l следует что:
Максимум интерференционной картины будет наблюдаться при условии синфазного сложения колебаний волн источников. синфазное сложение колебаний имеет место при условии кратности оптической разности хода целому числу длин волны в среде. Порядком интерференционного максимума называют его номер, отсчитываемый от центрального, которому соответствует центр интерференционной картины , где складываются волны от источников, проходящие одинаковый путь. Найти положения минимумов интерференционной картины двух источников можно если положить оптическую разность хода кратной нечётному числу полуволн. Положения соседних интерференционных максимумов и минимумов находятся на одинаковом расстоянии друг от друга и не зависят от того, насколько эти максимумы удалены от центра интерференционной картины.
Оптической длиной пути в однородной среде называется произведение расстояния, пройденного светом в среде с показателем преломления n, на показатель преломления: l = nS Для неоднородной среды необходимо разбить геометрическую длину на столь малые промежутки, что можно было бы считать на этом промежутке показатель преломления постоянным: dl = nds. Полная оптическая длина пути находится интегрированием:
7) Интерференция света в тонких пленках. Полосы равного наклона, полосы равной толщины.
Оптическая разность хода в тонких плёнках возникает из-за того, что первый луч отражается от границы раздела среды, при этом происходит сдвиг фазы на π.
Полосы равного наклона возникают при освещении пластинки расходящимся или расходящимся пучком монохроматического света, при этом каждая полоса проходит через точки слоя, на которых лучи попадают под одним углом φ. Эти полосы локализованы в бесконечности.
2nhcosy + l/2 = k l/2
(n — преломления показатель вещества пластинки; h — её толщина; l — длина волны света; y — угол преломления лучей; k — целое число, чётное значение которого соответствует максимумам, а нечётное — минимумам освещённости). Дополнительный член l/2 в выражении для разности хода учитывает сдвиг фаз при отражении от оптически более плотной среды
Полосы равной толщины наблюдаются при интерференции от пластинки переменной толщины. максимумы и минимумы освещённости полос совпадают с линиями на поверхности слоя, по которым разность хода интерферирующих лучей одинакова и равна целому числу l/2. На этих линиях одинакова геометрическая толщина слоя. Классическим примером полос равной толщины являются кольца Ньютона. Они соблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластины и плоско-выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой.
При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении- эллипсов. Найдем радиусы колец при нормальном падении света.
Т. к. ,-для светлых,- для темных.
, чем больше m , тем теснее расположены кольца. Для светлых колец . Более точный результат, если брать разность двух колец.
studfiles.net
Интерференция в тонких слоях - Оптика
Строгое решение интерференционных задач в общем виде представляет сложную проблему. Мы рассмотрим лишь несколько простейших случаев.
При изучении интерференции от точечных монохроматических источников область возможного наблюдения интерференции .определялась только размерами области перекрытия интерферирующих пучков. В реальных же условиях, как уже отмечалось, влияние конечных размеров источника и его немонохроматичности сильно ограничивает область наблюдаемости интерференции.
Рис 3.6.
Большой практический интерес представляет интерференция в тонких слоях, наблюдаемая на поверхности этих слоев. Оптическая схема наблюдений изображена на рисунке 3.6. Удаленный источник света (это необходимо для соблюдения условия 3.6) освещает тонкий слой с постепенно меняющейся толщиной. Лучи, сходящиеся в некоторой точке А поверхности слоя (например, верхней), падают на линзу, дающую на экране действительное изображение поверхности слоя. В зависимости от его толщины и длины волны света получаются различные освещенности (линии равной толщины). Реальная постановка опыта с тонкой мыльной пленкой, образованной на каркасе К отображена на рисунке 3.7, а; наблюдаемая картина и вертикальное сечение мыльной пленки показаны на рисунке 3.7,б, в.
Для расчета интерференции учтем (это будет показано в §5.1), что при образовании изображения идеальной линзой не возникает дополнительной разности хода лучей, идущих от точки отображаемой поверхности в точку экрана. Поэтому достаточно рассчитать разность хода лучей в точке А на поверхности пленки. Рассматривая бесконечно узкий участок слоя, мы можем считать его плоским (рис. 3.8). Для лучей 1 и 2 плоскость AA1 является волновым фронтом. На участке А1С, расположенном в вакууме (показатель преломления воздуха практически равен единице, и воздух можно формально заменить вакуумом), укладывается число длин волн, равное:
На участке АВС, лежащем внутри слоя с показателем преломления n, укладывается число длин волн λ1=λ/n, равное:
Наконец, следует учесть различие в условиях отражения в точках С и В, приводящее к возникновению дополнительного скачка фазы, т. е. дополнительной разности хода в полволны.
Рис. 3.7
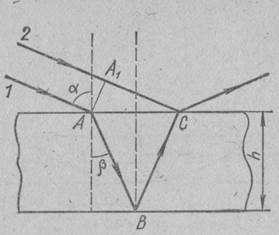
Рис 3.8
Действительно, из формул Френеля (2.4) для простейшего случая нормального падения волны получается такое выражение коэффициента отражения (по амплитуде):
При n>1r<0, при n<1r> 0. В первом случае (отражение от оптически более плотной среды в точке С) происходит скачок фазы на 180° («потеря полуволны»), во втором случае (отражение в точке В) скачок отсутствует.
Поэтому полная разность хода (оптическая) лучей 1 и 2, выраженная в длинах волн в вакууме, составит:
(3.7)
При получается максимум, при —минимум (m=0, 1, 2, …).
Таким образом, каждой толщине отвечает своя разность хода и, следовательно, своя интенсивность (при данной длине, волны, если углы р примерно одинаковы). Изображение пленки на экране оказывается перерезанным горизонтальными линиями разных (чередующихся) цветов. В верхней части пленка кажется черной, в нижней — более толстой — интерференция незаметна, пленка кажется прозрачной. Расстояния между полосами одного цвета уменьшаются сверху вниз. По мере испарения пленки и стекания мыльного раствора под действием силы тяжести картина непрерывно изменяется, причем расстояния между полосами растут.
Все эти результаты вполне понятны. Черный цвет пленки в верхней части связан с тем, что там толщина пленки много меньше длины полуволны и разность хода определяется только различием в условиях отражения света. Дальше толщина увеличивается, и начинает работать условие (3.7). Если бы пленка была в точности клинообразной, то расстояния между линиями одного цвета были бы одинаковы. Так как этого нет, то приходится признать, что. сечение пленки имеет форму, показанную на рисунке 3.7, г. Исчезновение интерференционной картины в толстой части пленки связано с немонохроматичностью света (см. условие 3.5).
Малейшее изменение толщины пленки влияет на интерференцию — это наводит на мысль о возможности использования интерференционных эффектов для измерения малых смещений.
Освещенность интерференционной картины не очень велика, так как коэффициент отражения света от прозрачной пленки с показателем преломления, не превышающим 1,5—2, относительно мал. Напомним (см. §2.4), что при нормальном падении коэффициент отражения (по энергии) равен:
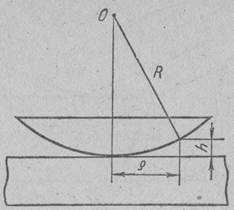
Рис 3.9
В проходящем свете может наблюдаться дополнительная картина— максимуму света в отраженной картине отвечает минимум (в проходящем свете), так как интерференция сводится к перераспределению светового потока, а не к изменению его значения. Но наблюдение в проходящем свете затруднено небольшой разницей освещенности в максимумах и минимумах.
Как уже указывалось, Ньютон наблюдал стационарную картину интерференции в тонком воздушном слое, образованном между поверхностями плоскопараллельной пластины и плоско-выпуклой линзы большого радиуса. Нижняя поверхность линзы отображалась на экран при помощи собирающей линзы (или же глаз фокусировался на эту поверхность). На рисунке 3.9 показана геометрия опыта, из которой следует, что в отраженном свете в центре картины должна быть минимальная освещенность (если контакт между обоими стеклами надежен), а вокруг должны получаться кольца.
При малых углах падения имеем:
(ρ — радиус темных колец). Радиусы растут с длиной волны. Из точных наблюдений Ньютона можно было (это сделали в XIX в. его последователи) вычислить длины световых волн.
Если шлифовка стекол несовершенна, то вместо окружностей получаются кривые сложной формы, позволяющие судить о качестве шлифовки и отклонении от заданной формы,— это находит практическое применение в технике.
Другой способ наблюдения интерференции в тонких пленках, также представляющий практический интерес, заключается в помещении экрана в фокальной плоскости отображающей линзы (или фокусировке глаза «на бесконечность»), В этом случае в каждой точке экрана собираются лучи определенного направления (рис. 3.10). Если тонкий слой освещается широким световым конусом, то, как легко понять, лучи, падающие под определенным углом, образуют в фокальной плоскости (если толщина слоя во всех точках одна и та же) кольцо, радиус которого зависит только от угла падения лучей, т. е. от bх наклона к поверхности слоя (см. уравнение 3.7). Поэтому такие кольца (или части их, если размеры поверхности невелики) называют «кривыми равного наклона».
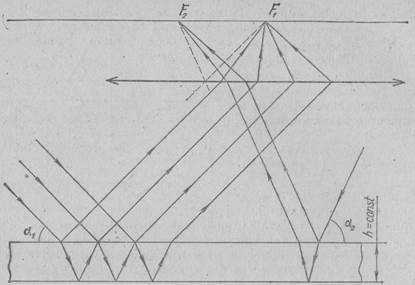
Рис. 3.10
В идеальном случае плоскопараллельного слоя, освещаемого параллельным монохроматическим пучком света, освещенность во всех точках фокальной плоскости должна быть одинакова.
Если толщина слоя нестрого одинакова, интерференционная картина усложняется, так как разность хода теперь зависит одновременно и от толщины, и от наклона лучей.
itteach.ru
Интерференция в тонких пленках.
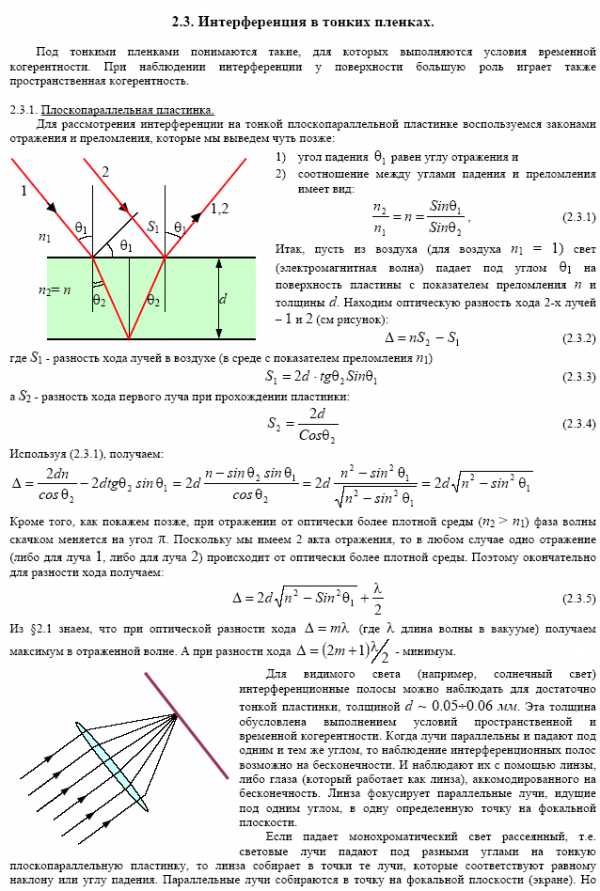


Полосы равной толщины.
Полосы равной толщины, один из эффектовоптики тонких слоев, в отличие отполос равного наклона, наблюдаются непосредственно на поверхности прозрачного слоя переменной толщины (рис. 1). Возникновение П. р. т. обусловленоинтерференцией света, отражённого от передней и задней границ слоя (П. р. т. в отражённом свете), или света, проходящего прямо через слой, с дважды отражённым на его границах (П. р. т. в проходящем свете). Полосами в строгом смысле (отчётливыми, попеременно тёмными и светлыми) обычно являются лишь П. р. т.монохроматическом светеили близком к нему (свете, длины волн которого заключены в сравнительно небольшом интервале). При этом максимумы и минимумы освещённости полос совпадают с линиями на поверхности слоя, по которымразность ходаинтерферирующих лучей одинакова и равна целому числу /2. На этих линиях одинакова геометрическая толщина слоя — отсюда название «П. р. т.». При освещениибелым светомналожение П. р. т., отвечающих лучам с разными , создаёт сложную радужно-цветовую картину, в которой П. р. т. лучей с отдельными зачастую неразличимы. П. р. т. обусловливают радужную окраску тонких плёнок (мыльных пузырей, масляных и бензиновых пятен на воде, плёнок окислов на металлах, в частностицвета побежалости, и пр.). Их используют для определения микрорельефа тонких пластинок и плёнок (рис. 2), в рядеинтерферометров и др. устройств для точных измерении (см., например,Ньютона кольцаи рис. к этой статье; кольца Ньютона — частный пример П. р. т.).
Рис. 1. Разность хода интерферирующих лучей, отражённых от верхней и нижней границ тонкого слоя, зависит от углов падения освещающих лучей. Однако разброс этих углов даже в случае протяжённых источников света обычно столь невелик, что разность хода, приобретаемая в точке М слоя лучами 1—1' и 2—2'; которые испущены разными участками (S1и S2) источника, практически одинакова. Поэтому полосы равной толщины локализованы непосредственно на поверхности слоя и их можно наблюдать без вспомогательных оптических устройств (линза на рис. может быть хрусталиком глаза). М' — точка на сетчатке глаза (или — при использовании дополнительной линзы — на экране), где фокусируется изображение точки М поверхности слоя, т. е, одной из точек линии равной толщины.
Рис. 2. Полосы равной толщины на поверхности слюдяной пластинки, характеризующие микрорельеф этой поверхности.
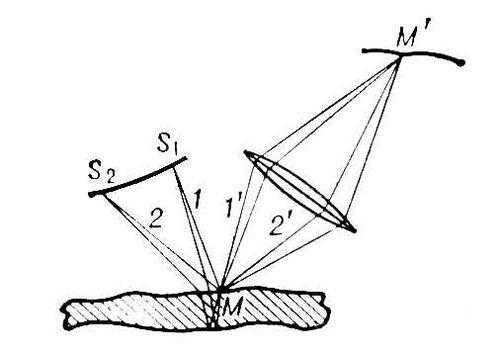

рис. 1 рис. 2
Кольца Ньютона.
Кольца Ньютона - интерференционная картина, возникающая в проходящем или отраженном свете в окрестности точки соприкосновении выпуклой поверхности с плоскостью.
После отражения лучей на границах раздела стекло-воздух и воздух стекло лучи интерферируют, образуют интерференционную картину в виде концентрических колец.
---------------------------------------------------------------------------------------------------------------------
Это оптическое явление, возникающее в тех случаях, когда в компьютер импортируется изображение с прозрачной пленки. Подобно радуге, появляющейся на поверхности мыльного пузыря, кольца появляются при плотном соприкосновении двух поверхностей, когда между ними возникает очень тонкий промежуток. Появляются, так называемые, интерференционные полосы. Чтобы избежать этого явления при сканировании прозрачных пленок, нужно класть пленку лицевой стороной прямо на стеклянную поверхность сканера.
studfiles.net
Интерференция в тонких пленках .
Пленкой будет называться прозрачный слой , толщина которого сравнима с длиной волны . Плоская монохроматическая волна падает на прозрачную пленку толщиной d и показателем преломления n под углом i . Луч 1 падающий на пленку в точке А , частично отразится (луч 1'), а частично преломится под углом r и войдет в пленку . Дойдя до точки D , он частично преломится в воздух (nвозд 1), а частично отразится от нижней грани пленки и пойдет к точке С . Здесь он опять частично отразится и преломится . Часть луча 1 снова выйдет в воздух в этой точке под углом i . Но в точку С попадет и частично отраженный под тем же углом луч 2 . На фронте АB оба луча имеют одинаковую фазу , но в дальнейшем проходят различные пути в различных средах. Оптическая разность хода, приобретаемая этими лучами, выразится:
Из рис. 2. видно , что
Учитывая , что , получим :
Известно , что при отражении света от оптически более плотной среды фаза колебаний сменяется на а оптическая разность хода на 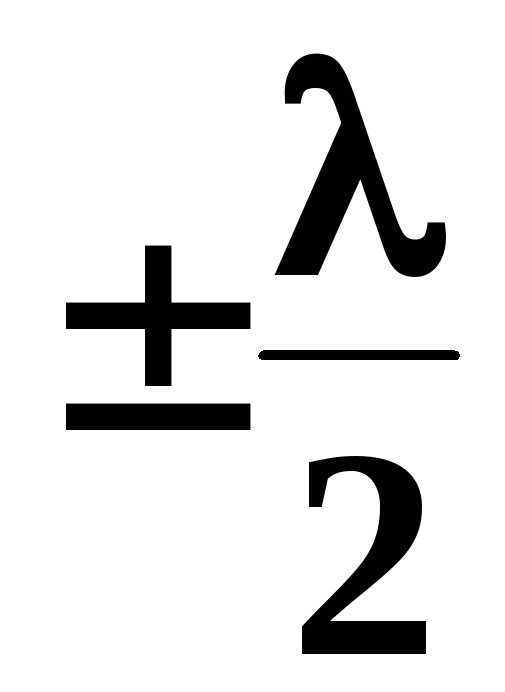 . В данном случае следует взять
. В данном случае следует взять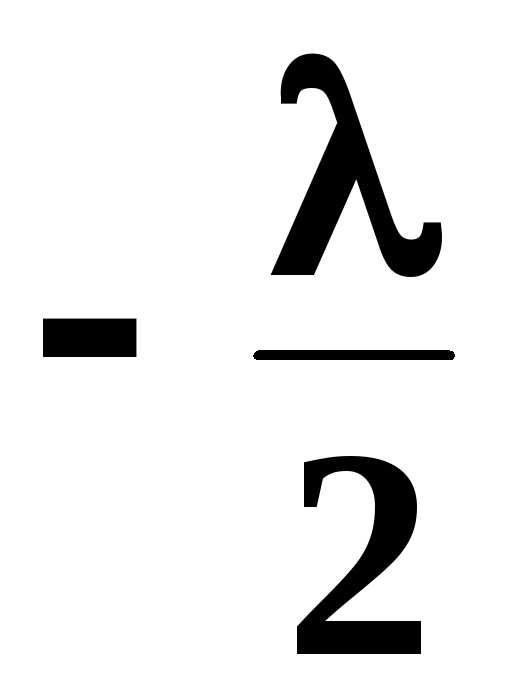 , т.к. отражение от более плотной среды происходит в точкеА , следовательно , « теряет » фазу луч 2 . Таким образом , при падении на пленку плоской волны образуется две отраженные волны , разность хода которых определяется выражением
, т.к. отражение от более плотной среды происходит в точкеА , следовательно , « теряет » фазу луч 2 . Таким образом , при падении на пленку плоской волны образуется две отраженные волны , разность хода которых определяется выражением
(7)
Эти волны могут интерферировать при соблюдении условий временной когерентности.
Если освещать пленку монохроматическим светом , то при выполнении условия
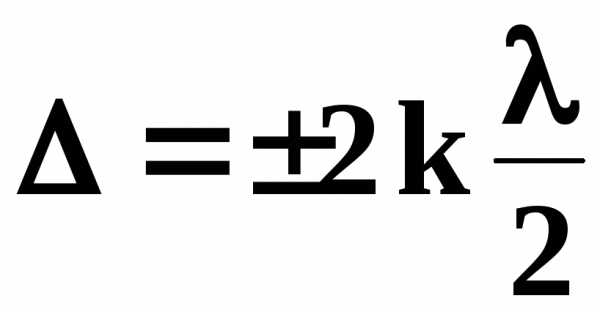 - условие максимума (8)
- условие максимума (8)
она будет иметь цвет источника монохроматического излучения .
При условии
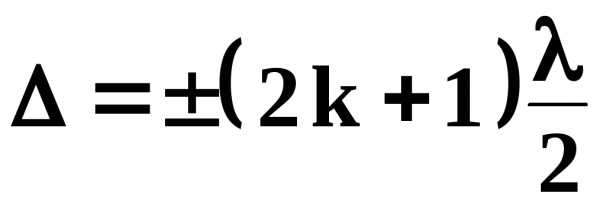 - условие минимума (9)
- условие минимума (9)
пленка будет темной .
При освещении пленки данной толщины белым светом под определенным углом максимум интерференции будет приходится на определенную длину волны , и пленка окажется окрашенной в цвет , соответствующий этой длине волны .
Полосы равного наклона .
Согласно (7) при освещении плоскопараллельной пленки ( d = const ) монохроматическим светом ( = const ) результаты интерференции в различных точках экрана зависят только от углов падения i . Все лучи падающие на пленку под определенным углом i = const ( например , луч S и все параллельные ему ) , соберутся на экране в одной точке С ( рис.3 ) . Лучи другого наклона ( например , лучи , параллельные S') соберутся в другой точке С'. В общем случае имеется семейство точек, для которых i = const , т.е. получится интерференционная полоса равного наклона . Так как положение максимумов зависит от длины волны ( условие 8 ) , то в белом свете получится совокупность смещенных друг относительно друга полос , образованных лучами разной длины волны , и интерференционная картина приобретает радужную окраску .
Полосы равной толщины .
Если пленка имеет переменную толщину , например , клин , и освещается параллельным пучком лучей , то разность хода определяется только толщиной пленки ( рис. 4 ) .Эта разность хода сохраняется постоянной только вдоль линий , параллельных ребру клина и убывает в направлении ребра клина. Поэтому поверхность пленки будет покрыта чередующимися светлыми и темными полосами, параллельными ребру называющимися полосами равной толщины. Частным случаем полос равной толщины являются кольца Ньютона .
Кольца Ньютона .
Если наложить сферическую линзу на плоское стекло , то получим воздушный слой ( n = 1 ) переменной толщины (рис. 5)
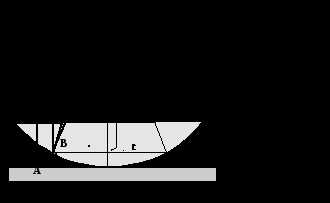
Интерференционные полосы , возникающие в такой системе , имеют вид концентрических окружностей , которые называются кольцами Ньютона .
Рассчитаем радиусы колец Ньютона . При нормальном падении лучей и большом радиусе кривизны R поверхности линзы можно пренебречь различными углами падения лучей на сферическую поверхность . Оптическая разность хода для данного случая
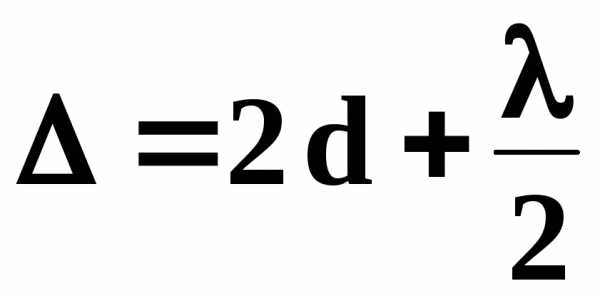 (10)
(10)
Из рис. 5 видно , что луч 1 отражается от оптически более плотной среды (точка А ) , а луч 2 - от оптически менее плотной среды (точка В), что ведет к возникновению дополнительной разности хода в полволны  . Темные кольца (минимумы освещенности ) образуются при условии
. Темные кольца (минимумы освещенности ) образуются при условии
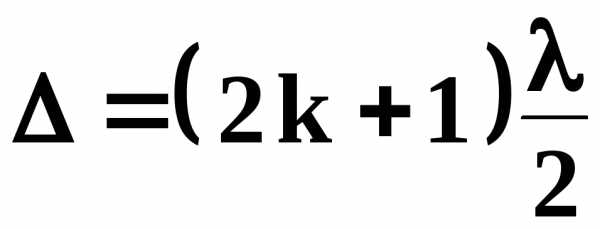
светлые - при условии
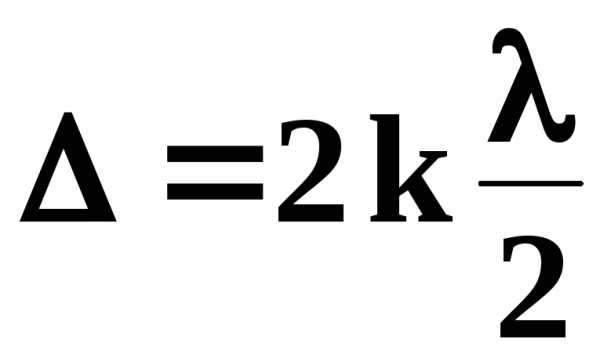
Толщина воздушного слоя d на расстоянии ( радиус кольца ) от центра “0” при радиусе кривизны линзы R определяется из геометрических соображений .
Пренебрегая членом 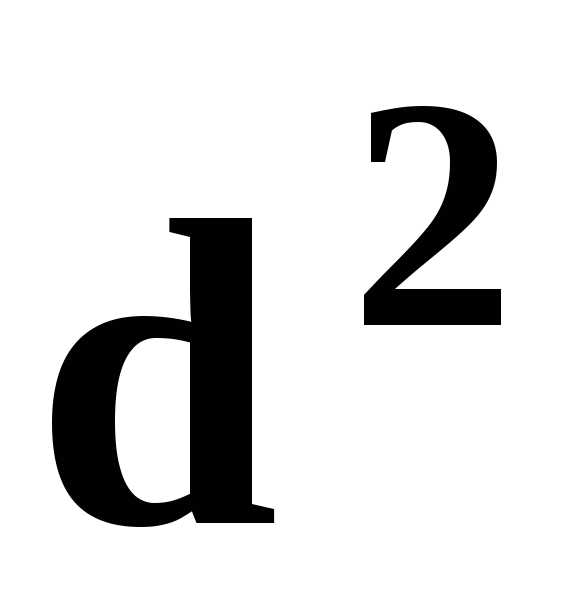 как очень малым по сравнению с2dr , находим
как очень малым по сравнению с2dr , находим 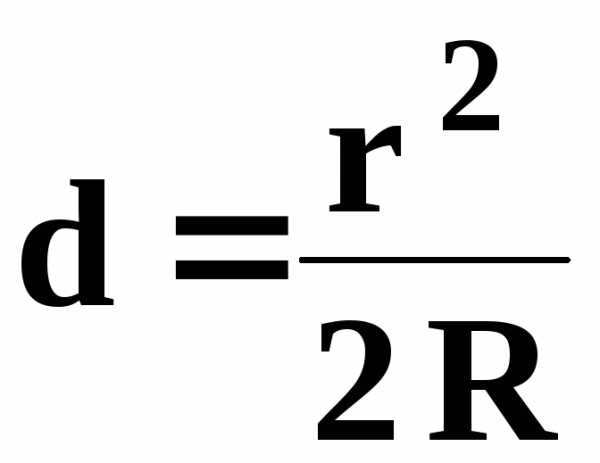
Подставляя это в (10) для темных колец будем иметь
( в отраженном свете ).
Отсюда радиусы этих колец равны
, (k = 0,1,2,3...)
где k - порядковый номер темного кольца .
Для светлых колец имеем 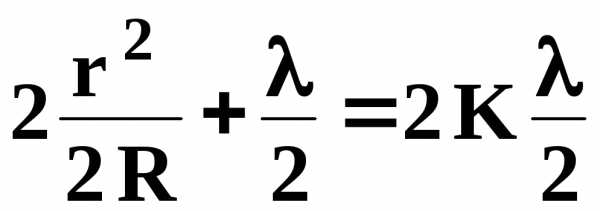
Отсюда радиусы светлых колец
( k = 0,1,2,3...)
Измеряя радиусы колец Ньютона и зная длину волны света , можно рассчитать радиус кривизны сферической поверхности линзы .
Если известен радиус кривизны линзы, то измеряя радиусы колец в интерференционной картине , можно с большой точностью измерить длину волны падающего на линзу монохроматического света .
Таким образом , интерференционные полосы образуют концентрические окружности с темным пятном ( минимумом ) в середине - месте контакта . Это следует из выражения (10) , т.к. при 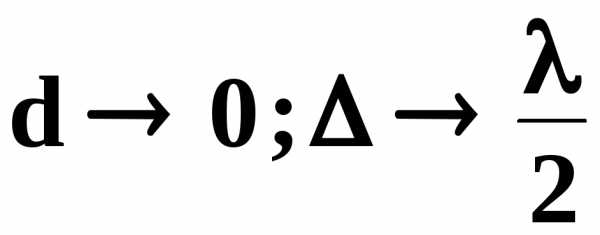 и , следовательно , колебания происходят в противофазе и гасят друг друга .
и , следовательно , колебания происходят в противофазе и гасят друг друга .
На практике трудно обеспечить контакт линзы с пластинкой в точке “0”, поэтому для расчетов обычно измеряют радиусы двух колец с номерами i и k .
Отсюда
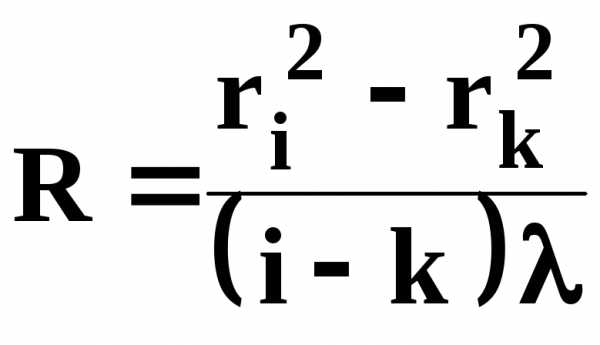 (11)
(11)
Экспериментальная установка и обработка результатов .
Вопытах используется микроскоп , на столике которого размещена линзаЛ, установленная на плоской пластинке с зачерненной нижней поверхностью (рис. 6) . Свет от источника S через конденсатор K и светофильтр Ф направляется на полупрозрачную пластинку P .От пластинки лучи попадают на воздушный слой . Затем лучи , отраженные от верхней и нижней поверхности воздушного слоя , попадают в объектив микроскопа . Микроскоп фокусируется на верхнюю поверхность пластинки. По шкале микроскопа измеряют радиусы r' колец Ньютона. Картина, наблюдаемая в микроскопе, есть увеличенное изображение действительных колец Ньютона. Радиусы действительных колец можно вычислить, зная увеличение микроскопа. В нашем случае увеличение равно 56, поэтому истинный радиус кольца равен
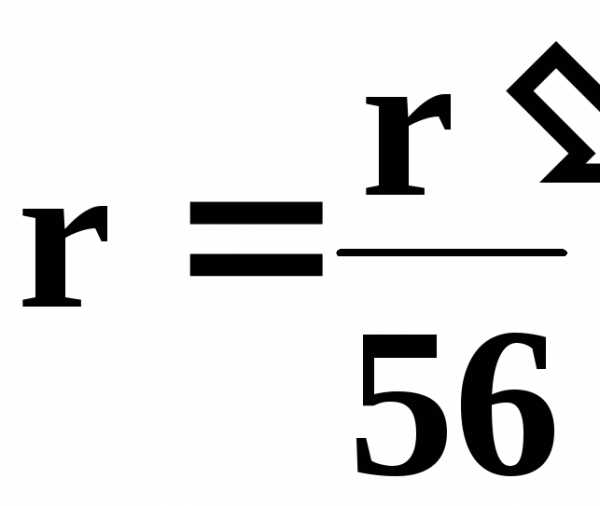
Зная радиусы колец , по формуле (11) можно вычислить R. Данные вносим в таблицу :
| № п / п | № колец | r', мм | r, мм | , мм | R, мм |
| 1 2 3 | |||||
| Ср. |
studfiles.net












