На мыльную пленку падает белый свет
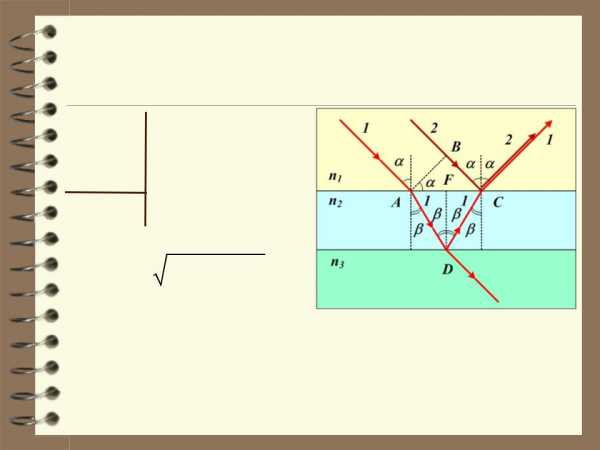
4. На мыльную плёнку падает белый свет под углом i = 45 к
Дано: i = 45º
λ = 600 нм n = 1,33
h - ?
d =2hn1 n1 =1,
|
| Решение |
|
|
| ||||
Согласно |
| условию | |||||||
плёнка | находится | в | |||||||
воздухе. n1 = n3 =1, |
|
| |||||||
n2 | = |
|
| 1,33. Тогда | |||||
оптическая разность | |||||||||
хода лучей 1 и 2 равна | |||||||||
n212 - sin2 a - | l | . | |||||||
2 | |||||||||
| = | n2 | =n, |
| |||||
n21 |
| a =i. | |||||||
|
| ||||||||
|
|
| n1 |
|
| ||||
В точке D отражение происходит от оптически менее плотной среды, фаза волны не изменяется, а в точке С – от оптически более плотной среды, поэтому вычитаем λ/2.
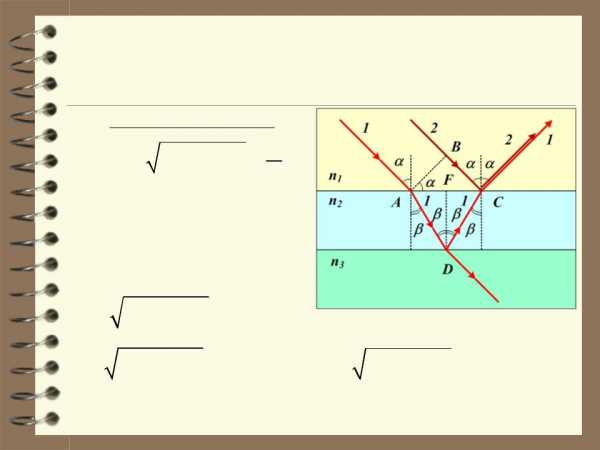
4. На мыльную плёнку падает белый свет под угломi = 45 к поверхности плёнки. При какой наименьшей толщине плёнки отражённые лучи будут окрашены в жёлтый цвет ( = 600 нм)?
Решение (продолжение)
d =2h n2 - sin2 i -l2 .
Плёнка окрашена в жёлтый цвет, |
|
|
|
| |||||||
следовательно, | для | волн, |
|
|
|
| |||||
соответствующих жёлтому свету ( λ |
|
|
|
| |||||||
= 600 нм) наблюдается максимум. |
|
|
|
| |||||||
| d =ml. | l |
|
|
|
|
|
|
| ||
2h | n2 - sin | 2 i - | =ml, |
|
|
|
| ||||
2 |
| ( | ) |
|
| ||||||
|
|
|
| 2 |
| 2 |
| ||||
|
|
|
|
|
|
| |||||
2h | n2 - sin2 i =ml | + | l | , | 2h n2 - sin2 i = | 2m +1 | l | , | |||
|
| ||||||||||
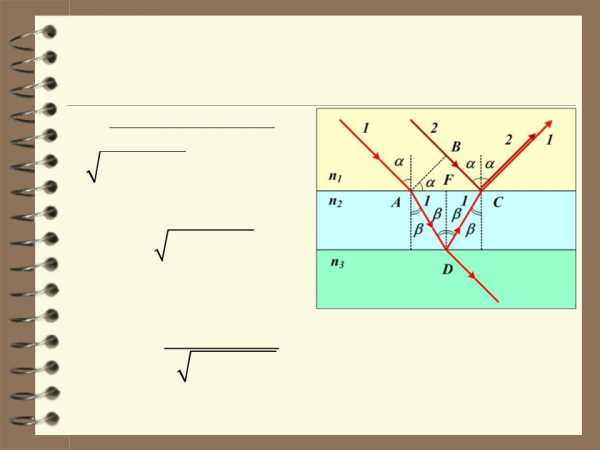
4. На мыльную плёнку падает белый свет под угломi = 45 к поверхности плёнки. При какой наименьшей толщине плёнки отражённые лучи будут окрашены в жёлтый цвет ( = 600 нм)?
Решение (продолжение)
| ( | ) | 2 |
| |
2h n2 - sin2 i = | 2m +1 | l | , | ||
| |||||
h = | (2m +1)l | . |
|
| |
|
|
| |||
| 4 n2 - sin2 i |
|
| ||
Толщина плёнки минимальна, поэтому m = 0.
l |
|
h =4n2 - sin2 i | » 0,13ì êì . |
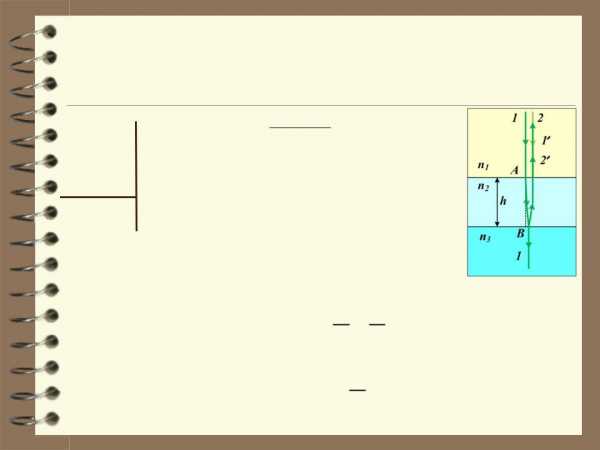
15. На поверхность стеклянного объектива (nc = 1,5) нанесена тонкая плёнка,
показатель преломления которой n = 1,2. При какой наименьшей толщинеh этой плёнки произойдёт максимальное ослабление отражённого света в средней части видимого спектра (λ = 550 нм)?
Дано:
λ = 550 нм
nп = 1,2 nс = 1,5
h - ?
Решение
Максимальное ослабление отражённого света будет, если в отражённом свете наблюдается минимум интенсивности на заданной длине
поэтому следует добавить (или вычесть) λ/2 и к оптической длине луча 1 (отражение от границы плёнка – стекло) и к оптической длине луча 2 (отражение от границы воздух
плёнка). Итого оптическая разность хода
d =L1 -L2 =2hn2 +l2 -l2 =2hn2.
Условие минимума интенсивности:
d =(2m +1) l2 .
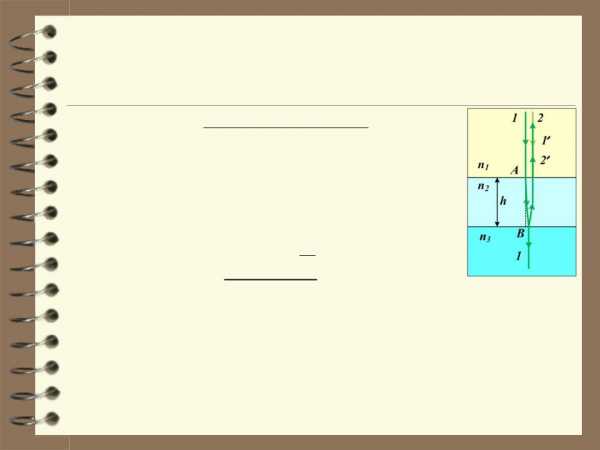
15. На поверхность стеклянного объектива (nc = 1,5) нанесена тонкая плёнка,
показатель преломления которой n = 1,2. При какой наименьшей толщинеh этой плёнки произойдёт максимальное ослабление отражённого света в средней части видимого спектра (λ = 550 нм)?
Решение (продолжение)
( | ) | 2 |
|
| d = | 2 | |
d = | 2m +1 | l | , |
| 2hn. | ||
| ( | ||||||
|
| 2 | ) | 2 |
| ||
| 2hn | = | 2m +1 | l | . | ||
|
| ||||||
(2m +1)l
h =2 . 2n2
Толщина плёнки h будет минимальной приm = 0.
hmin= | l | =0,55×10- 6 | » 0,12×10- 6 ì =0,12ì êì . | |
4n2 | ||||
| 4×1, 2 |
|
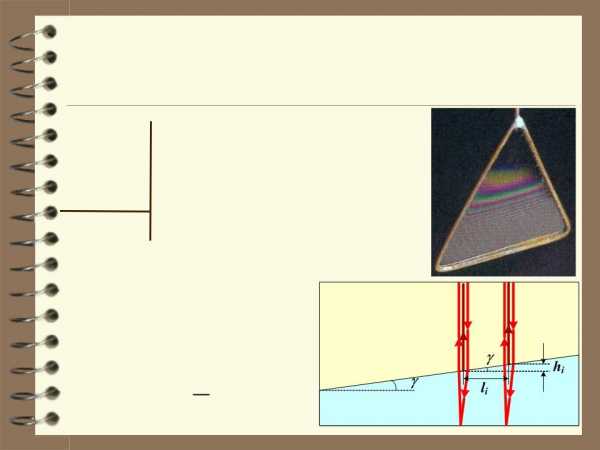
5. Мыльная плёнка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном свете ртутной дуги ( = 546,1 нм) оказалось, что расстояние между пятью полосамиl = 2 см. Найти угол клина. Свет падает перпендикулярно к поверхности плёнки.
Дано: |
|
| Решение |
| |||||
λ = 546,1 нм |
|
|
|
|
|
|
| ||
Положение | светлых | полос в | |||||||
nп = 1,33 |
| ||||||||
| отражённом |
| свете |
| определяется | ||||
li = 2 см |
| условием |
|
| максимума | для | |||
i = 5 |
| интерференцииd =ml . |
| ||||||
- ? |
|
|
|
|
|
|
|
| |
Оптическая разность хода определяется толщиной | |||||||||
мыльной плёнки |
| l |
|
|
|
| |||
d =L1 | - L2 =2dn - | . |
|
|
| ||||
|
|
|
| ||||||
|
|
| 2 |
|
|
|
| ||
Таким образом, условие максимума в отражённом свете
2dn- l2 =ml.
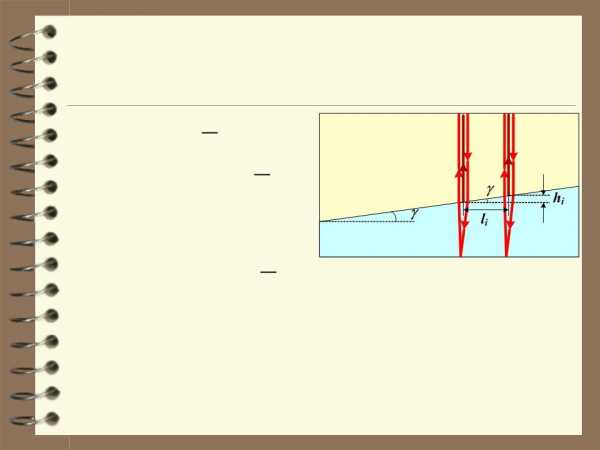
5. Мыльная плёнка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном свете ртутной дуги ( = 546,1 нм) оказалось, что расстояние между пятью полосамиl = 2 см. Найти угол клина. Свет падает перпендикулярно к поверхности плёнки.
2dn- l =ml,
=(2 + )l
2dn 2m 12 .
Толщина плёнки в точке, соответствующей максимуму
dm =(2m +1) l .
2n 2
Величина hi есть разность двух значений толщины плёнки, соответствующих разным максимумам:
h =d | m+i | - d | m | =(2m +2i +1) | l | - (2m +1) | l | = | 2i |
| l | = | il | . |
|
|
|
|
|
| |||||||||
i |
| 2n | 2 | 2n 2 2n 2 2n | ||||||||||
|
|
|
| |||||||||||
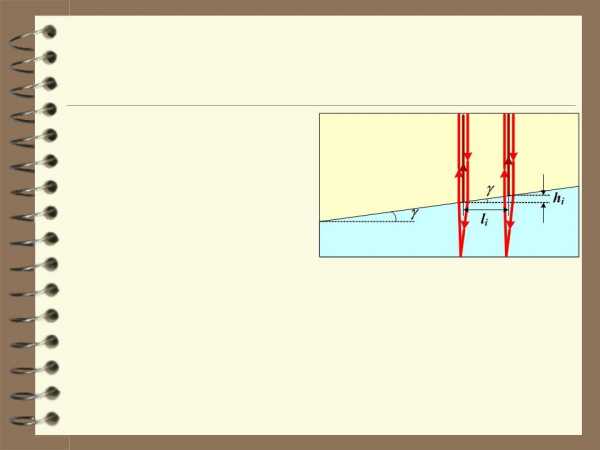
5. Мыльная плёнка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном свете ртутной дуги ( = 546,1 нм) оказалось, что расстояние между пятью полосамиl = 2 см. Найти угол клина. Свет падает перпендикулярно к поверхности плёнки.
Из прямоугольного треугольника на |
|
|
|
| |||||||||
рисунке |
|
|
|
|
|
|
|
| |||||
|
| tgg =hi . |
|
|
|
|
| ||||||
|
|
|
|
| l |
|
|
|
|
| |||
| g ® 0, | i |
|
|
|
|
| ||||||
| tgg =g. |
|
|
|
|
| |||||||
|
| g =hi = | il | . |
|
|
|
|
| ||||
|
|
|
|
|
|
| |||||||
|
|
| l |
| 2nl |
|
|
|
|
| |||
|
|
|
| i |
| i |
|
|
|
|
| ||
g |
| il |
|
| 5×546,1×10- 9 |
| 5,13 10- 5 |
| 2,94 10- 3 | 10¢ | |||
=2nli =2×1,33×2×10- 2 | » | » | |||||||||||
| × | × °» |
| ||||||||||
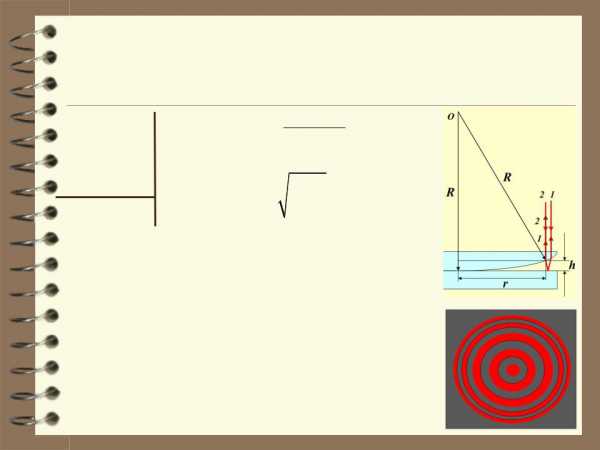
6. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отражённом свете. Радиусы двух соседних тёмных колец равныrk = 4,0 мм и
rk+1 = 4,38 мм. Радиус кривизны линзыR = 6,4 м. Найти порядковый номер колец и длину волны падающего света.
Дано:
rk = 4,0 мм
rk+1 = 4,38 мм R = 6,4 м
n - ? λ - ?
Решение
Радиус тёмного кольца номер k в
отражённом | свете |
|
| определяется | ||||||
формулой | rk = kR | l | . |
|
|
| ||||
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| |||
|
|
|
|
| n |
|
|
| ||
Для колец номер k иk+1 |
| l |
| |||||||
2 |
| l |
| r2 | = k +1R | . | ||||
| ||||||||||
rk | =kRn , |
| ||||||||
k +1 | ( | ) | n | |||||||
r2 | - r 2 | = | Rl |
| |||
k +1 | k |
| n |
|
|
|
l = | (rk2 | 1 - rk2 )n | » | × | - 7 |
|
|
| rk2 ×n |
|
+ |
| ì . | k = |
| =5. | |||||
|
| 5 10 |
| Rl | ||||||
|
| R |
|
|
|
|
|
|
| |
|
|
|
| (Для | n = 1) |
|
|
|
| |
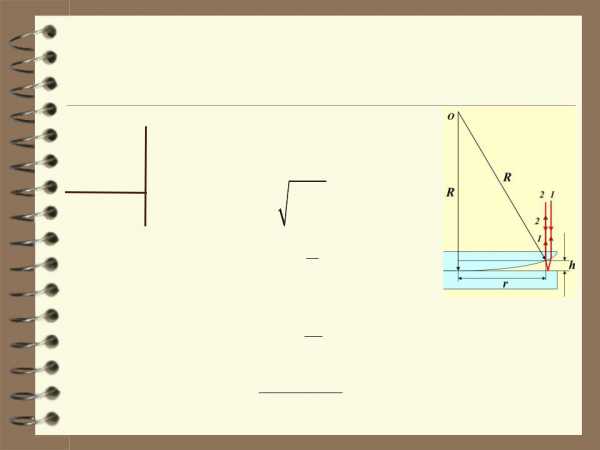
10. Установка для наблюдения колец Ньютона освещена светом с длиной волны λ = 589 нм, падающим по нормали к поверхности пластинки. Радиус кривизны линзыR = 10 м. Пространство между линзой и пластинкой
заполнено жидкостью. Найти показатель преломления жидкости, если радиус | ||||||
третьего светлого кольца в проходящем свете равен r3 = 3,65 мм. | ||||||
Дано: |
|
| Решение |
| ||
|
|
|
|
|
| |
r3 = 3,65 мм | Радиус светлого кольца номер k в | |||||
λ = 589 нм | проходящем |
| свете | определяется | ||
R = 10 м | формулой | = kR | l |
|
| |
| rk | . |
| |||
n - ? |
|
| ||||
|
|
| n |
| ||
rk2 =kRln .
Отсюда показатель преломления жидкости
n =kRl2 . rk
n =3×10×5892×10- 9 6 »1,33. 3,65 ×10×-
studfiles.net
| birmaga.ru | 1 КОНТРОЛЬНАЯ РАБОТА № 3 1. На мыльную пленку падает белый свет под углом 45°. При какой наименьшей толщине пленки отраженные лучи будут окрашены в зеленый цвет (λ = 0,54 мкм)? Показатель преломления мыльной воды 1,33. 2. На щель шириной 0,3 мм. падает нормально параллельный пучок монохроматического света с длиной волны 0,45 мкм. Найти ширину центрального дифракционного максимума на экране, удаленном от щели на 1 м.
|
birmaga.ru
| www.birmaga.ru | 1 КОНТРОЛЬНАЯ РАБОТА № 3 1. На мыльную пленку падает белый свет под углом 45°. При какой наименьшей толщине пленки отраженные лучи будут окрашены в зеленый цвет (λ = 0,54 мкм)? Показатель преломления мыльной воды 1,33. 2. На щель шириной 0,3 мм. падает нормально параллельный пучок монохроматического света с длиной волны 0,45 мкм. Найти ширину центрального дифракционного максимума на экране, удаленном от щели на 1 м.
|
www.birmaga.ru