4.5. Интерференция света в тонких пленках. Разность хода лучей в тонкой пленке

Интерференция в тонких пленках, теория и примеры

Мы часто наблюдаем радужное окрашивание тонких пленок, например, масляные пленки на воде, пленки оксидов на металлах, которые появляются, как результат интерференции света, который отражают две поверхности пленки.

Интерференция в тонких пленках

Рассмотрим плоскопараллельную тонкую пластину, показатель преломления которой равен n, а толщина равна b. Пусть на такую пленку под углом падает плоская монохроматическая волна (допустим, что это один луч) (рис.1). На поверхности такой пленки, в некоторой точке А луч делится. Он частично отражается от верхней поверхности пленки, частично преломляется. Преломлённый луч доходит до точки B, частично преломляется в воздух (показатель преломления воздуха равен единице), частично отразится и пойдет к точке С. Теперь он снова частично отразится и преломится, выйдет в воздух под углом . Лучи (1 и 2), которые вышли из пленки являются когерентными, если оптическая разность хода их мала в сравнении с длинной когерентности падающей волны. В том случае, если на пути лучей (1 и 2) поставить собирающуюся линзу, то они сойдутся в некоторой точке D (в фокальной плоскости линзы). При этом возникнет картина интерференции, которая определена оптической разностью хода интерферирующих лучей.

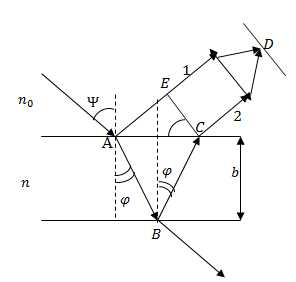
Рис. 1

Оптическая разность хода лучей 1 и 2, которая появляется у лучей при прохождении ими расстояния от точки А до плоскости CE, равна:

где считаем, что пленка находится в вакууме, поэтому показатель преломления . Возникновение величины объясняется потерей половины длины волны при отражении света от гарницы раздела сред. При половина волны будет потеряна в точке А, и при величине будет стоять знак минус. Если , то половина волны будет потеряна в точке В и при будет стоять знак плюс. В соответствии с рис.1:

где – угол падения внутри пленки. Из того же рисунка следует, что:

Примем во внимание, что для рассматриваемого случая закон преломления:

имеем:

Учитывая потерю половины длины волны:

Для случая, при котором , получим:

По условию для максимумов интерференции, в точке D мы будем наблюдать максимум, если:

где

Минимум интенсивности будет наблюдаться в рассматриваемой точке, если:

где

Явление интерференции может наблюдаться только, если удвоенная толщина пленки меньше, чем длины когерентности падающей волны.

Выражения (8) и (9) показывают, что картина интерференции в пленках определена толщиной пленки ( у нас b), длиной волны падающего света, показателем преломления вещества пленки и углом падения (). Для перечисленных параметров каждому наклону лучей () соответствует своя интерференционная полоса. Полосы, возникающие в результате интерференции лучей, падающих на пленку под одинаковыми углами, носят названия полос равного наклона.

Примеры решения задач

ru.solverbook.com

физика / КОМПЛЕКТ_ДЛЯ_ЗО / Лекции / Лекция 3 / Лекция 3

9

Лекция 3

Вопросы

1. Расчет интерференционной картины от двух источников.

2. Интерференция света в тонких пленках.

3. Кольца Ньютона.

4. Применение интерференции света

1. Расчет интерференционной картины от двух источников

Интенсивность в любой точке М экрана, лежащей на расстоянии х от точки 0, определяется разностью хода

Δ = L2  L1 (1)

;

;

Так как l >> d, то L2 + L1  2l и

. (2)

Условие максимума Δ = mλ; (m = 0, ±1, ±2, ...)

. (3)

Условие минимума 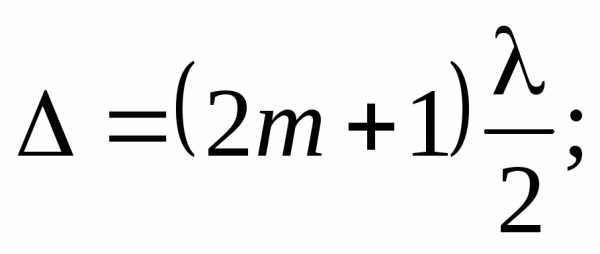(m = 0, ±1, ±2, ...)

. (4)

Шириной интерференционной полосы называется расстояние между двумя соседними максимумами (или минимумами)

, (5)

ширина интерференционной полосы 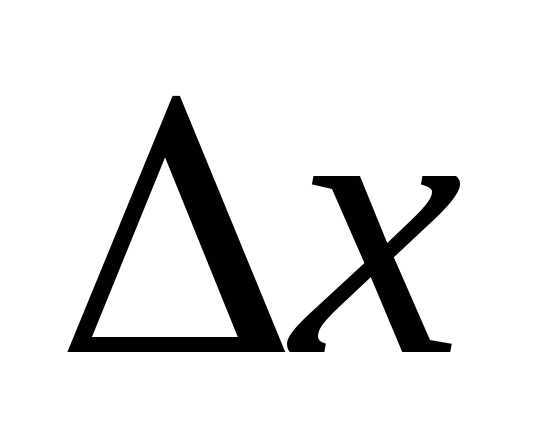не зависит от порядка интерференцииm и является постоянной. Главный максимум интерференции при m = 0  в центре, от него  максимумы первого (m = 1), второго (m = 2) и т. д. порядков.

Для видимого света 10-7 м , 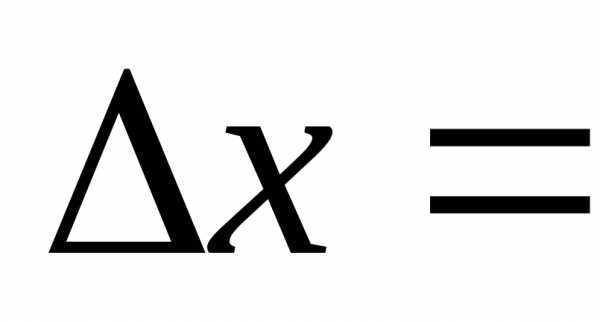0,1 мм = 10-4 м (разрешающая способность глаза) интерференция наблюдается при l/d = x/ > 103.

При использовании белого света с набором длин волн от фиолетовой ( = 0,39 мкм) до красной ( = 0,75 мкм) границ спектра при m = 0 максимумы всех волн совпадают, далее при m = 1, 2, …  спектрально окрашенные полосы, ближе к белой  фиолетовый, дальше  красный.

2. Интерференция света в тонких пленках

Интерференцию света можно наблюдать не только в лабораторных условиях с помощью специальных установок и приборов, но и в ес­тественных условиях. Так, легко наблюдать радужную окраску мыльных пленок, тонких пленок нефти и минерального масла на поверхности воды, оксидных пленок на поверхности закаленных стальных деталей (цвета побежалости). Все эти явления обусловле­ны интерференцией света в тонких прозрачных пленках, возникающей в результате наложения когерентных волн, возникающих при отражении от верхней и нижней по­верхностей пленки.

Оптическая разность хода лучей 1 и 2

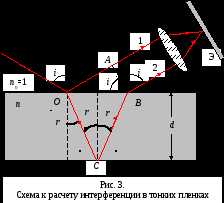
где п – показатель преломления пленки; n0 – показатель прелом­ления воздуха, n0 = 1; λ0/2 – длина полуволны, потерянной при от­ражении луча 1 в точке О от границы раздела с оптически более плотной средой (n>n0,).

;

;

;

.

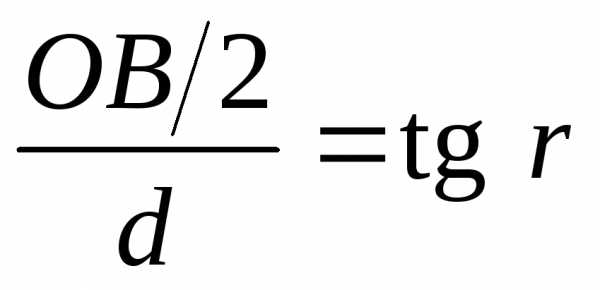
. (7)

Условие максимума

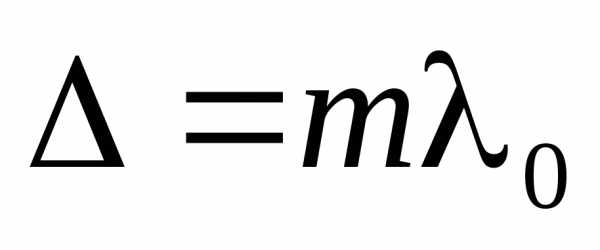: (8)

Условие минимума

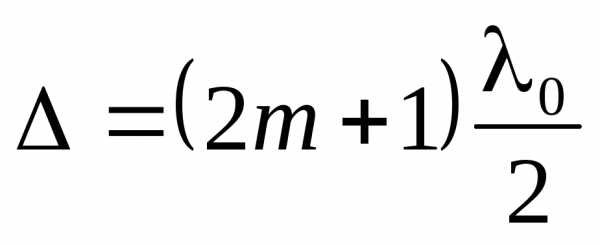: (9)

При освещении пленки белым светом она окрашивается в какой-либо определенный цвет, длина волны которого удовлетворяет макси­муму интерференции. Следовательно, по цвету пленки можно оцени­вать её толщину.

Полосами равного наклона называют интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами.

Полосами равной толщины называют интерференционные полосы, возникающие в результате наложения лучей, падающих на пластинку переменной толщины от мест одинаковой толщины.

3. Кольца Ньютона

Кольца Ньютона  классический пример полос равной толщины.

В отраженном свете оптическая разность хода (с учетом потери полуволны λ0/2 при отражении от плоскопараллельной пластинки):

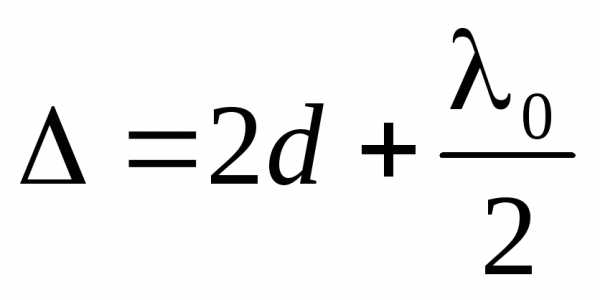, (10)

где d – ширина зазора.

R2 = r2 + (R – d)2

(d << R)

.

. (11)

Условие максимума радиус светлого кольца

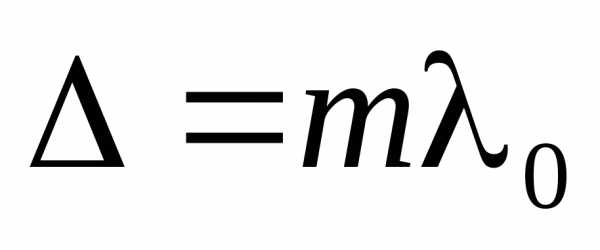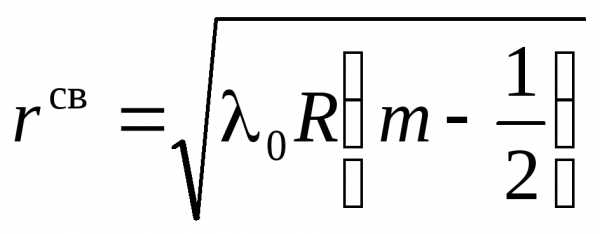: (12)

Условие минимума радиус темного кольца

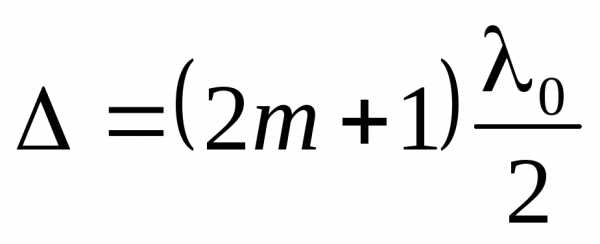: (13)

Система светлых и темных полос получается только при освеще­нии монохроматическим светом. В белом свете интерференционная картина изменяется,  каждая светлая полоса превращается в спектр.

Кольца Ньютона можно наблюдать и в проходящем свете. При этом максимумы интерференции в отраженном свете соответствуют ми­нимумам в проходящем и наоборот.

Измеряя радиусы колец Ньютона, можно определить λ0 (зная радиус кривизны линзы R ) или R (зная λ0 ).

4. Применение интерференции света

4.1. Интерференционная спектроскопия измерение длин волн.

4.2. Улучшение качества оптических приборов («просветленная оптика») и получение высокоотражающих покрытий.

Толщину пленки d и показатели преломления стекла nст и пленки ппл подбирают так, чтобы при интерфе­рен­ции в отраженном свете лучи 1 и 2 гасили друг друга. Для этого их оптическая разность хода должна удовлетворять условию

, (14)

;

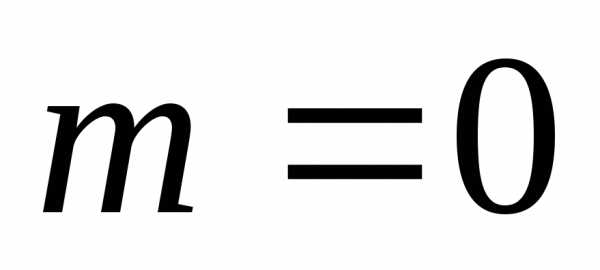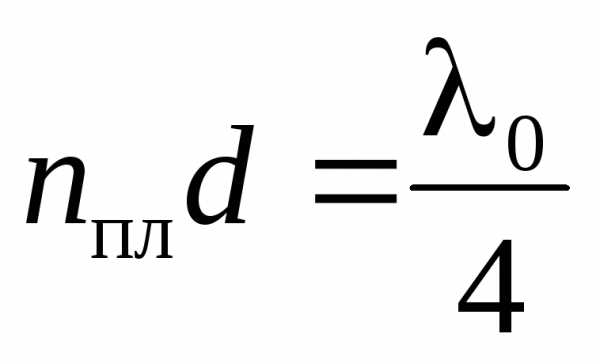
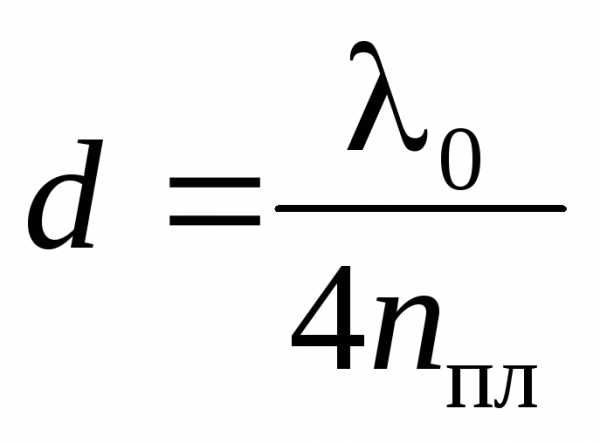. (15)

Так как добиться одновременного гашения всех длин волн спектра не­возможно, то это обычно делается для зеленого цвета (λ0 = 550 нм), к которому человеческий глаз наиболее чувствителен (в спектре из­лучения Солнца эти лучи имеют наибольшую интенсивность).

В отраженном свете объективы с просветленной оптикой кажутся окрашенными в красно-фиолетовый цвет. Для улучшения характеристик просветляющего покрытия его делают из нескольких слоев, что «про­светляет» оптические стекла более равномерно по всему спектру.

4.3. Интерферометр  прибор, служащий для точного (прецизионного) измерения длин, углов, показателей преломления и плотности прозрачных сред и т.д.

Интерференционная картина очень чувствительна к разности хо­да интерферирующих волн: ничтожно малое изменение разности хода вызывает заметное смещение интерференционных полос на экране.

Все интерферометры основаны на одном и том же принципе - делении одного луча на два когерентных - и различаются лишь кон­структивно.

S  источник света;

Р1 полупрозрачная пластин­ка;

Р2 прозрачная пластина;

М1, М2 зеркала.

Лучи 1′ и 2′ когерентны, следовательно, наблюдается интерферен­ция, результат которой будет зависеть от оптической разности хода луча 1 от точки 0 до зеркала М1 и луча 2 от точки 0 до зеркала М2. По изменению интерференционной картины можно судить о малом перемещении одного из зеркал. Поэтому интерферометр Майкельсона применяется для точных (~ 10-7 м) измерений длин.

Самый известный эксперимент, выполненный Майкельсоном (совместно с Морли) в 1887 г., ставил целью обнаружить зависимость скорости света от скорости движения инерциальной системы координат. В результате было установлено, что скорость света одинакова во всех инерциальных системах, что послужило экспериментальным обоснованием для создания специальной теории относительности Эйнштейна.

Интерференционный дилатометр  прибор для изменения длины тела при нагревании.

Советский физик академик В.П. Линник использовал принцип действия интерферометра Майкельсона для создания микроинтерферометра (комбинация интерферометра и микро­скопа), служащего для контроля чистоты обработки поверхности ме­таллических изделий. Таким образом, интерферометр Линника является прибором, пред­назначенным для визуальной оценки, измерения и фотографирования высот микронеровностей поверхности вплоть до 14-го класса чистоты поверхности.

Другим чувствительным оптическим прибором является рефрактометр  интерферометр Рэлея. Он применяется для определения незначительных изменений показателя преломления прозрачных сред в зависимости от давления, температу­ры, примесей, концентрации раствора и т.д. Интерферометр Рэлея позволяет измерять изменение показателя преломления c очень высокой точностью  Δn ~ 10 -6 .

studfiles.net

Интерференция в тонких пленках

Количество просмотров публикации Интерференция в тонких пленках - 501

Явление интерференции в тонких пленках широко наблюдается в естественных условиях: радужная окраска мыльных пузырей, нефтяных пленок, масляных пятен на поверхности воды, крыльев бабочки.

В этом случае интерферируют лучи, полученные от отражения падающего луча от верхней и нижней поверхностей. Оптическая разность хода между лучами не велика из-за малой толщины пленки и в связи с этим они принадлежат одному цугу, а значит когерентны.

Для установления общих закономерностей интерференции света в тонких пленках рассмотрим плоскопараллельную прозрачную пленку толщиной , на которую под углом = падает монохроматическая волна. Будем предполагать, что по обе стороны от пленки находиться воздух. Абсолютный показатель преломления пленки больше чем у воздуха.

Падающая волна частично отражается от поверхности пленки (луч 1) и частично преломляется (луч OC). Преломленная волна, достигнув нижней поверхности пленки, отражается от нее (луч CB). Луч CB затем преломляется на верхней поверхности (луч 2). Лучи 1 и 2 с помощью линзы собираются на экране в точке и интерферируют. Результат интерференции зависит от оптической разности хода между лучами 1 и 2.

Оптическая разность хода между двумя интерферирующими лучами от точки O до плоскости AB равна: , где - показатель преломления пленки, член обусловлен потерей полуволны при отражении света от границы раздела с оптически более плотной средой. Расстояния OA, OC и CB находится геометрическим методом (, рис.1):

, .

Учитывая, что , получим:

.

Выразим оптическую разность хода через величину угла . Учитывая, что , получим:

.

Из этого выражения следует, что интерференционная картина в тонких пленках зависит от величин , , и . Для заданных , и каждому наклону лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей падающих на плоско-параллельную пластинку под одинаковыми углами, называются полосами равного наклона (рис.2).

Читайте также

referatwork.ru

Интерференция в тонких пленках.

Пластинка постоянной толщины. При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при определенных условиях могут интерферировать.

Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна (параллельный пучок света) (рис.17.4). В результате отражений от поверхностей пластинки, часть света возвращается в исходную среду.

В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.

Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S1 и S2 источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.

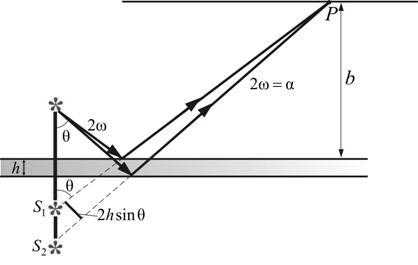
Рис. 17.4

Полосы равного наклона.Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 17.5).

В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точке P такая же, как на линии DC:

.

Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е. . Так как , (h – толщина пластинки, и – углы падения и преломления на верхней грани; ), то для разности хода получаем

.

Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:

,

где – длина волны в вакууме.

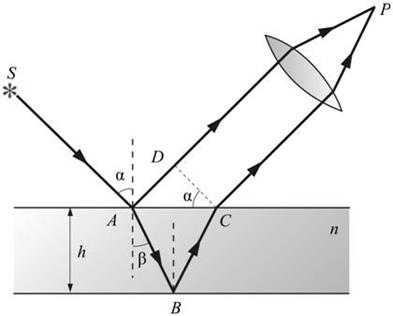
Рис.17.5

В соответствии с последней формулой светлые полосы расположены в местах, для которых , где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.

Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.

Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис.17.6). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя , дает , а луч 2, отражаясь от з2 и далее от , дает . Пластинки и одинаковы по размерам. ставится для компенсации разности хода второго луча. Лучи и когерентны и интерферируют.

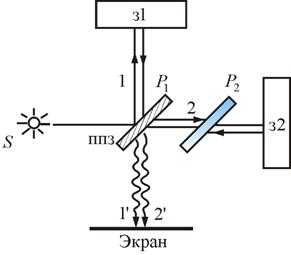
Рис. 17.6

Полосы равной толщины (интерференция от клина). Мы рассмотрели интерференционные опыты, в которых деление амплитуды световой волны от источника происходило в результате частичного отражения на поверхностях плоскопараллельной пластинки. Локализованные полосы при протяженном источнике можно наблюдать и в других условиях. Оказывается, что для достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Возникающие при этих условиях полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.

Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина).

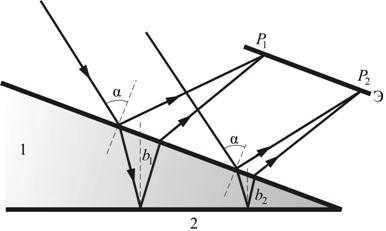
Рис. 17.7

Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают (рис.17.7). Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость).

Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности.

Результат интерференции в точках и экрана определяется по известной формуле , подставляя в неё толщину пленки в месте падения луча ( или ). Свет обязательно должен быть параллельным ( ): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет.

Рис.17.8

Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис.17.8). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.

Кольца Ньютона.На рис.17.9 изображена оправа, в которой зажаты две стеклянные пластины. Одна из них слегка выпуклая, так что пластины касаются друг друга в какой-то точке. И в этой точке наблюдается нечто странное: вокруг нее возникают кольца. В центре они почти не окрашены, чуть дальше переливаются всеми цветами радуги, а к краю теряют насыщенность цветов, блекнут и исчезают.

Так выглядит эксперимент, в XVII веке положивший начало современной оптике. Ньютон подробно исследовал это явление, обнаружил закономерности в расположении и окраске колец, а также объяснил их на основе корпускулярной теории света.

Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла называют кольцами Ньютона.

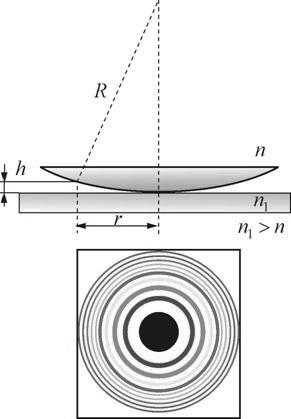Рис. 17.9

Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны , разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π. Толщина h воздушного зазора связана с расстоянием r до точки касания:

.

Здесь использовано условие . При наблюдении по нормали темные полосы, как уже отмечалось, соответствуют толщине , поэтому для радиуса m-го темного кольца получаем

(m = 0, 1, 2, …).

Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света.

Итак, полосы равного наклона получаются при освещении пластинки постоянной толщины рассеянным светом, в котором содержатся лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) параллельным пучком света. Полосы равной толщины локализованы вблизи пластинки.

Просветление оптики

Одной из важных задач, возникающих при построении различных оптических и антенных устройств СВЧ-диапазона, является уменьшение потерь ( ) интенсивности света, мощности потока электромагнитной энергии при отражении от поверхностей линз, обтекателей антенн и пр. приборов, используемых для преобразований световых и радиоволн в разнообразных приборах фотоники, оптоэлектроники и радиоэлектроники. Для уменьшения потерь на отражение используется покрытие оптических деталей (линз) 3 пленкой 2 со специальным образом подобранными толщиной δ и показателем преломления n (рис. 17.10).

Идея уменьшения интенсивности отраженного света от поверхности оптических деталей состоит в интерференционном гашении волны, отраженной от внешней поверхности детали 1, волной отражённой от внутренней 2. Для осуществления этого амплитуды обеих волн должны быть равны, а фазы отличаться на 180°. В этом случае обеспечивается гашение отражённой волны. Необходимое соотношение между фазами отражённых волн обеспечивается выбором толщины плёнки δ, кратной нечётному числу четвертей длины волны проходящего через рассматриваемую деталь света: .

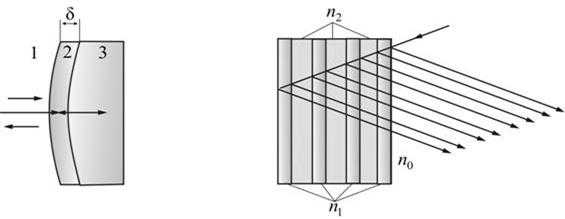
Рис. 17.10

Таким образом, если выполняется данное условие, то в результате интерференции наблюдается гашение отраженных лучей.

Так как добиться одновременного гашения для всех длин волн невозможно, то его делают для . Поэтому объективы с просветленной оптикой кажутся голубыми.

Рекомендуемые страницы:

lektsia.com

Интерференция в тонких пленках. — МегаЛекции

При освещении тонкой плёнки или пластинки происходит наложение световых волн, отразившихся от передней и задней поверхностей плёнки. Эти две волны получаются делением волны, идущей от одного источника S (см. рис.4). Для плоскопараллельной пластинки постоянной толщины интерференционная картина наблюдается в фокальной плоскости линзы, собирающей отражённые от верхней и нижней граней пластинки пучки лучей 1 и 2.

Лучи 1 и 2 образуются из падающего на пластинку луча SA. От источника S до точки А между ними разность хода отсутствует. Линия DC, перпендикулярная лучам 1 и 2, представляетсобойволновую поверхность, т.е. поверхность постоянной фазы.

Линза не вносит дополнительной разности хода для параллельных лучей, а лишь преобразует плоскую волну в сходящуюся сферическую волну. Поэтому после перпендикуляра DC, опущенного на лучи 1 и 2, до точки наложения лучей Р разность хода между лучами 1 и 2 также не возникает.

Оптическая разность хода между лучами 1 и 2 возникает из-за того, что первый луч прошел, отразившись от границы раздела воздух-среда, отрезок AD в воздухе, а второй луч прошел путь АВС от точки А до точки С в пластинке с показателем преломления n и отразился от границы раздела среда-воздух.

При отражении световой волны от оптически более плотной среды (отражение луча 1 в точке А) фаза отраженной волны изменяется на противоположную (т.е. на π). Это можно представить как возникновение разности хода равной половине длины волны для первого луча. При отражении волны от оптически менее плотной среды (отражение луча 2 в точке В) изменения фазы не происходит, и соответственно разности хода не возникает.

Поэтому колебания в точку С (волновая поверхность DC) приходят оптическими путями: L1 = n(AB + ВС) и L2 = AD + λ/2 . Отсюда можно записать, что оптическая разность хода, возникающая между лучами 1 и 2 от источника S до точки наложения лучей Р будет равна:

∆ = L 1 - L2 = n (АВ + ВС) - (AD + λ /2) = 2nАВ - AD – λ /2 (19)

Отрезки AD и АВ удобнее выразить через толщину пластинки (d) и угол падения луча ( i ) или угол преломления луча (r), используя треугольники ABE и ACD:

из треугольника ABE АВ = d / cos r, ЕВ = d tg r (20)

из треугольника ADC AD = AC sin i, AC = 2EB = 2d tg r,

∆= 2nd/Cos r – AC Sin i = 2nd /Cos r - 2dtg rsin i = 2nd / Cos r - 2dSin r /Cos r Sin i = 2d/Cos r (n - Sin r Sin i )

по закону преломления света на границе двух сред Sin i = n Sin r, тогда

Δ = 2d/Cos r (n - nSin2r),умножим левую половину равенства на n\n

Δ= 2d/nCos r.(n2 - n2 Sin2r) ,из тригонометрии знаем, что ,

тогда, если то получим:

(21)

вспомним, что n · Sin r = Sin i, тогда , учтём изменение фазы отражённого луча на λ⁄2и получим:

(22)

2.5.Вывод рабочей формулы определения радиуса кривизны линзы

Интерференционные полосыравной толщины в тонкой пленке, т.е. темные или светлые полосы соответствующие постоянному значению толщины пленки (d), можно наблюдать в воздушной прослойке между соприкасающимися друг с другом плоской поверхностью пластинки и выпуклой сферической поверхностью линзы (см. рис.5).

При этом толщина воздушной прослойки постепенно увеличивается от центра линзы к ее краям. При нормальном (перпендикулярном поверхности) падении света полосы равной толщины имеют вид концентрических окружностей, которые получили названиеколец Ньютона.

Если на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней границ воздушной прослойки, интерферируют между собой.

Так как, в отличии от выше приведённого примера, отражение световой волны происходит в точке В от раздела среды воздух-стекло, а не стекло-воздух, как на рис.4,то λ/2 добавляется к слагаемому L1 и формула (19), в начальной её части приобретёт вид:

∆ = L1- L2 = (АВ + ВС + λ/2) - AD = 2d + λ/2

То есть, оптическая разность хода, в этом случае равна удвоенной толщине воздушного зазора (2d) ( показатель преломления воздуха n = 1).

В итоге получим:

∆ = 2d + λ/2 . (23)

Рис.5. Схема возникновения Рис.6. Учет деформации

колец Ньютона линзы

Тёмные кольца образуются там, где оптическая разность хода равна нечётному числу полуволн (см.16):

∆ = 2d + λ /2 = (2m + 1) λ /2, (24)

т.е. при толщине зазора

d = m λ /2 , (25)

где m = 0,1,2,3... - номер кольца.

Радиус m-ного темного кольца (rm ) определяется из треугольника AОС (см.рис.5)

rm2= R2 - (R - d,)2 = 2Rd – d 2, (26)

где R - радиус кривизны линзы. Полагая величину воздушного зазора в месте возникновения колец малой, (т.е. d « R) можно записать:

rm2 = 2Rd. (27)

Из этой формулы видно, что радиус кривизны линзы можно найти, измерив радиус кольца Ньютона и величину воздушного зазора в месте возникновения кольца. Радиус колец Ньютона можно измерить, воспользовавшись микроскопом, имеющим измерительную шкалу. Чтобы не измерять величину зазора (кстати, не понятно, как это сделать экспериментально), можно воспользоваться интерференционным условием возникновения темных колец (24).

Тогда радиус кривизны линзы можно выразить через радиус кольца Ньютона, длину волны используемого света и номер измеряемого кольца:

rm2 = Rmλ (28)

Использование формулы (28) для определения радиуса кривизны может привести к ошибке, т.к. в точке соприкосновения линзы и стеклянной пластинки возможна деформация линзы по величине сравнимая с длиной волны света, поэтому использование выводов, основанных на рис.5 (см. формулы 26,27,28), будет некорректным.

Экспериментально наблюдаемая величина воздушного зазора может быть меньше теоретической величины, полученной из рис.5 на величину деформации стеклянной пластинки и линзы (δ) (см. рис.6). Поэтому в реальном эксперименте в формулу (27) вместо толщины воздушного зазора (d) необходимо подставить сумму толщины воздушного зазора и величины деформации линзы и стеклянной пластинки (d + δ). Учитывая, что условие возникновения темного кольца (24) определяется лишь толщиной зазора, получим следующую формулу, связывающую радиусы колец Ньютона с радиусом кривизны линзы:

rm2 = Rmλ + 2Rδ (29)

Экспериментально удобнее вместо радиуса кольца Ньютона измерять его диаметр (Dm ). В этом случае формула (29) будет иметь вид:

D m2 = 4Rmλ + 8Rδ, (30)

Из (30) видно, что квадрат диаметра кольца Ньютона (Dm2) пропорционален порядковому номеру кольца (m). Если построить график зависимости Dm2= f(m), то экспериментальные точки должны лежать на одной прямой, и тангенс угла наклона этой прямой (α) будет равен 4Rλ. Таким образом, для нахождения радиуса кривизны линзы необходимо, используя график зависимости Dm2 = f(m), найти

, (31)

а затем рассчитать радиус кривизны линзы по формуле:

R=tgα/4λ(32)

Вследствие деформации в центре линзы наблюдается круглое темное пятно, соответствующее нулевой толщине воздушного зазора. Измерив диаметр центрального темного пятна (кольца Ньютона, номер которого m = 0), можно найти величину деформации линзы по формуле:

δ= D02/8R(33)

Описание установки (Рис.7 и 8) и методика выполнения работы.

Интерференционная картина наблюдается с помощью микроскопа.

Свет от источника 1, пройдя светофильтр 3, становится монохроматическим и попадает на линзу 8, помещенную на стеклянную пластинку 9.

Диаметры колец Ньютона измеряются с использованием микрометрав микроскопе ‘Эликон’и по делениям шкалы окулярав микроскопеМБС-9,иопределяются разницей чисел делений, приходящихся на левый и правый края измеряемого кольца.

3.1.1. Измерение диаметров колец микроскопом ‘Эликон’ (Рис.7).

В фокальной плоскости окуляра микроскопа расположены неподвижная шкала с делениями от 0 до 8 и подвижные перекрестие и индекс в виде биштриха..

При вращении микрометрического винта (барабана) перекрестие и биштрих перемещаются в поле зрения окуляра относительно неподвижной шкалы. При повороте барабана на один оборот, биштрих и перекрестие, в поле зрения окуляра, переместятся на одно деление шкалы.

Барабан по окружности разделён на 100 делений. Поворот барабана на 1 деление соответствует перемещению перекрестия на 0,01 деления неподвижной шкалы. Полный отсчёт по шкале окулярного микрометра складывается из отсчета по неподвижной шкале и отсчета по барабану

На Рис.7 биштрих находится между делениями "5" и "6" неподвижной шкалы, а микрометрический барабан находится, к примеру, на делении "35" (напротив неподвижного индекса).

Следовательно, полный отсчёт составляет: 500 + 35 = 535 делений. Диаметры колец определяются разницей чисел делений, приходящихся на левый и правый края измеряемого кольца.

Для перевода делений в мм необходимо ввести коэффициент К, учитывающий кратность увеличения микроскопа.

3.1.2 Измерение диаметров колец микроскопом МБС−9 (Рис.8).

В фокальной плоскости окуляра микроскопа расположены перекрестие и шкала с делениями от 0 до 18. Кольца Ньютона проецируются в центр перекрестия. Диаметры колец определяются разницей чисел делений, приходящихся на левый и правый края измеряемого кольца.

На Рис.8 правый край нулевого кольца находится на делении 105, а левый−на делении 75.

Для перевода делений в мм необходимо ввести коэффициент К, учитывающий кратность увеличения микроскопа.

Рис.7. Микроскоп “Эликон : 1−источник света, 2 – конденсор, 3 – светофильтр, 4 – полупрозрачное зеркало, 5 – объектив, 6 – окуляр, 7 – шкала.

Объект исследования: 8–линза,9–стеклянная пластина.

Рис.8. Микроскоп МБС−9: 1−источник света, 2−конденсор, 3−светофильтр, 4 − призма, 5 – блок масштабирования, 6 – окуляр, 7 – шкала, 10−объектив.

Объект исследования:8–линза, 9–стеклянная пластина.

Рекомендуемые страницы:

Читайте также:

Воспользуйтесь поиском по сайту:

megalektsii.ru

Оптика и волны

Радужная окраска мыльных пузырей или бензиновых пленок на воде возникает в результате интерференции солнечного света, отраженного двумя поверхностями пленки.

Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом  падает плоская монохроматическая волна с длиной   (рис. 4.8).

Рис. 4.8. Интерференция света в тонкой пленке

Интерференционная картина в отраженном свете возникает из-за наложения двух волн, отраженных от верхней и нижней поверхностей пленки. Рассмотрим сложение волн, выходящих из точки С. Плоскую волну можно представить как пучок параллельных лучей. Один из лучей пучка (2) непосредственно попадает в точку С и отражается (2')в ней наверх под углом, равным углу падения . Другой луч (1) попадает в точку С более сложным путем: сначала он преломляется в точке А и распространяется в пленке, затем отражается от нижней ее поверхности в точке 0 и, наконец, выходит, Преломившись, наружу (1') в точке С под углом, равным углу падения . Таким образом, в точке С пленка отбрасывает вверх два параллельных луча, из которых один образовался за счет отражения от нижней поверхности пленки, второй — вследствие отражения от верхней поверхности пленки. (Пучки, возникающие в результате многократного отражения от поверхностей пленки, не рассматриваются ввиду их малой интенсивности.)

Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна

Полагая показатель преломления воздуха  и учитывая соотношения

и

а также

находим

Используем закон преломления света

откуда

Таким образом,

Кроме оптической разности хода , следует учесть изменение фазы волны при отражении. В точке С на границе раздела «воздух – пленка» происходит отражение от оптически более плотной среды, то есть среды с большим показателем преломления. При не слишком больших углах падения в этом случае фаза претерпевает изменение на . (Такой же скачок фазы происходит при отражении волны, бегущей вдоль струны, от ее закрепленного конца.) В точке 0 на границе раздела «пленка - воздух» свет отражается от оптически менее плотной среды, так что скачка фазы не происходит.

В итоге между лучами 1' и 2' возникает дополнительная разность фаз , соответствующая, как следует из формулы (4.12), оптической разности хода  , которую можно учесть, если величину  уменьшить или увеличить на половину длины волны в вакууме.

Следовательно, при выполнении соотношения

получается максимум интерференции в отраженном свете, а в случае

в отраженном свете наблюдается минимум.

Таким образом, при падении света на бензиновую пленку на воде в зависимости от угла зрения и толщины пленки наблюдается радужная окраска пленки, свидетельствующая об усилении световых волн с определенными длинами l. Интерференция в тонких пленках может наблюдаться не только в отраженном, но и в проходящем свете.

Как уже отмечалось, для возникновения наблюдаемой интерференционной картины оптическая разность хода интерферирующих волн не должна превышать длины когерентности , что накладывает ограничение на толщину пленки.

Пример. На мыльную пленку (п = 1.3), находящуюся в воздухе, падает по нормали пучок белого света. Определим, при какой наименьшей толщине d пленки отраженный свет с длиной волны  мкм окажется максимально усиленным в результате интерференции.

Из условия интерференционного максимума (4.28) находим для толщины пленки выражение

(угол падения ). Минимальное значение d получается при :

online.mephi.ru

Интерференция света в тонких пленках

При падении световой волны на тонкую прозрачную пленку или пластину имеет место отражение от обеих поверхностей пленки.

В результате возникают когерентные световые волны, которые обусловливают интерференцию света.

Пусть на прозрачную плоскопараллельную пленку с показателем преломления n и толщиной d под углом и падает плоская монохроматическая волна. Падающая волна частично отражается от верхней поверхности пленки (луч 1). Преломленная волна, частично отразившись от нижней поверхности пленки, на верхней поверхности вновь частично отражается, а преломленная волна (луч 2) накладывается на первую отраженную волну (луч 1). Параллельные лучи 1 и 2 когерентны между собой, они дают локализованную на бесконечности интерференционную картину, которая определяется оптической разностью хода. Оптическая разность хода для проходного света отличается от оптической разности хода для отраженного света на, так проходящий свет не отражается от оптически густой среды. Таким образом, максимумам интерференции в отраженном свете соответствуют минимумы интерференции в проходящем свете, и наоборот.

Интерференция монохроматического света на плоскопараллельной пластинке определяется величинами ?0, d, n, и и. Разным углам падения и отвечают разные точки интерференционной картины (полосы). Интерференционные полосы, возникающие в результате наложения волн, падающих на плоскопараллельную пластину под одинаковыми углами, называют полосами одинакового наклона. Параллельные лучи 1 и 2 сходятся в бесконечности, поэтому говорят, что полосы одинакового наклона локализованы на бесконечности. Для их наблюдения используют собирательную линзу и экран, расположенный в фокальной плоскости линзы.

6.4.2. Рассмотрим интерференцию света на клинообразной пленке переменной толщины. Пусть на клин с углом ? между боковыми гранями падает плоская волна (лучи 1, 2 на рис. 6.10). Очевидно, что отраженные лучи 1 ? и 1 ? ? от верхней и нижней поверхностей клина (так же как 2 ? и 2 ? ?) когерентные между собой. Они могут интерферировать. Если угол ? мал, то оптическая разность хода лучей 1 ? и 1. 

где dm - средняя толщина клина на участке АС. Из рис. 6.10 видно, что интерференционная картина локализована у поверхности клина. Система интерференционных полос возникает за счет отражения от мест пленки имеют одинаковую толщину. Эти полосы называются полосами одинаковой толщины. Пользуясь (6.21), можно определить расстояние ?у между двумя соседними максимумами для случая монохроматического света, нормального падения лучей и малого угла ?:

Частным случаем полос одинаковой толщины являются кольца Ньютона, возникающие в воздушной прослойке между Плосковыпуклая линзой большого радиуса кривизны R и плоской стеклянной пластиной, которые соприкасаются в точке Р. При наложении отраженных волн возникают интерференционные полосы одинаковой толщины, имеющие при нормальном падении света вид концентрических колец. В центре картины находится интерференционный минимум нулевого порядка. Это обусловлено тем, что в точке Р разность хода между когерентными лучами определяется только потерей полуволны при отражении от поверхности пластины. Геометрическим местом точек одинаковой толщины воздушной прослойки между линзой и пластиной есть круг, поэтому интерференционная картина наблюдается в виде концентрических темных и светлых колец.В проходящем свете наблюдается дополняющая картина - центральный круг светлое, следующее кольцо темное и т. д.Найдем радиусы светлых и темных колец. Пусть d - толщина воздушного слоя на расстоянии r от точки Р. Оптическая разность хода ? между лучом, который отбился от пластины, и лучом, который потерпел отражения на границе раздела выпуклая поверхность линзы - воздух. Очевидно, что в проходящем свете формулы (6.22) и (6.23) меняются местами. Экспериментальные измерения радиусов колец Ньютона позволяют рассчитать по этим формулам радиус Плосковыпуклая линзы R. Изучая кольца Ньютона в целом, нельзя давать оценку качеству обработки поверхностей линзы и пластины. Следует заметить, что при наблюдении интерференции в белом свете интерференционная картина приобретает радужной расцветки.

6.4.3. Явление интерференции света лежит в основе работы многочисленных оптических приборов - интерферометров, с помощью которых с большой точностью измеряют длину световых волн, линейные размеры тел и их изменение, а также измеряют показатели преломления веществ.В частности, на рис. 6.12 изображена схема интерферометра Майкельсона. Свет от источника S падает под углом 450на полупрозрачную пластину Р1. Половина падающего пучка света отражается в направлении луча 1, половина проходит через пластину в направлении луча 2. Пучок 1 отражается зеркалом М1 и, возвращаясь назад, снова проходит через пластину Р1 (). Пучок света 2 идет к зеркалу М2, отражается от него и, отразившись от пластины Р1, идет в направлении луча 2 ?. Поскольку луч 1 проходит через пластину Р1 трижды, а луч 2 только один раз, то для компенсации разности хода на пути луча 2 относится пластина Р2 (такая же как и Р1, но без полупрозрачного покрытия).

Интерференционная картина зависит от положения зеркал и геометрии пучка света, падающего на прибор. Если падающий пучок параллельный, а плоскости зеркал М1 и М2 почти перпендикулярны, то в поле зрения наблюдаются интерференционные полосы равной толщины. Смещение картинки на одну полосу соответствует смещению одного из зеркал на расстояние Таким образом, интерферометр Майкельсона используется для точных измерений длины. Абсолютная погрешность при таких измерениях составляет ? 10-11 (м). Интерферометр Майкельсона можно использовать для измерения малых изменений показателей преломления прозрачных тел в зависимости от давления, температуры, примесей.

А. Смакула разработал способ просветления оптических устройств для уменьшения потерь света, обусловленных его отражением от Заломного поверхностей. В сложных объективах число отражений велико, поэтому потери светового потока довольно значительны. Чтобы элементы оптических систем сделать просветленными, их поверхности покрывают прозрачными пленками, показатель преломления которых меньше, чем стекла. При отражении света на границе раздела воздух-пленка и пленка-стекло возникает интерференция отраженных волн. Толщину пленки d и показатели преломления стекла nc и пленки n подбирают так, чтобы отраженные волны гасят друг друга. Для этого их амплитуды должны быть ровными, а оптическая разность хода соответствовать условию минимума.

worldofscience.ru

• 
  Можно ли наклеить пленку на пленку
• 
  Зачем бисквит заворачивать в пищевую пленку
• 
  Какая пленка пароизоляционная для кровли лучше
• 
  У кота глаза затягивает белой пленкой
• 
  Строительные пленки пароизоляция гидроизоляция ветрозащита мембрана
• 
  Прозрачная пленка на глазу у собаки
• 
  Бронирование стекол фар автомобиля пленкой цена
• 
  Как снять пленку клейкую со стекла
• 
  Бронирование автомобиля защитной пленкой во владимире
• 
  Пленка фолдер для стен каркасного дома
• 
  Пленка матовая белая stm 70 wps