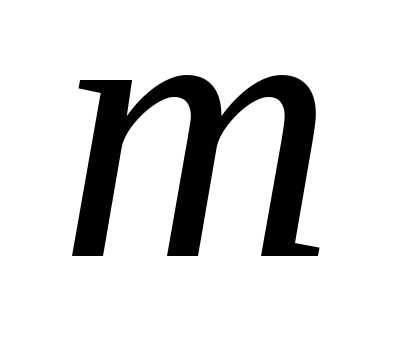Лабораторная работа № 5.0 экспериментальное изучение интерференции света в тонких пленках – кольца ньютона. Кольца ньютона интерференция в тонких пленках
Интерференция в тонких пленках. Кольца Ньютона.
Дом Интерференция в тонких пленках. Кольца Ньютона.
просмотров - 317
При падении светового пучка на тонкую пленку под углом α происходит его разделение на две волны, направления которых обозначены лучами 1 и 2 (рис.16.9). Волна 1 отражается от верхней границы пленки, волна 2 преломляется, отражается он нижней границы пленки, преломляется на верхней границе пленки и выходит из пленки. Эти волны являются когерентными волнами, которые образуются из одной первичной волны и проходят разный оптический путь. При наложении этих волн они интерферируют и результат интерференции зависит от оптической разности хода этих волн. В случае если на пленку падает белый свет, состоящий из световых волн разной длины волны, то условию максимума (16.6) при интерференции будут удовлетворять только волны какой- то определенной длины. По этой причине на поверхности пленки под разными углами зрения будут наблюдаться разноцветные радужные полосы. Эти полосы называются полосами равного наклона.
В случае если свет падает на пленку с переменной толщиной и отражается от нее (рис.16.10), то условие максимума (16.6) при интерференции лучей 1 и 2 будет выполняться только для определенных толщин d пленки. На поверхности пленки образуются яркие полосы, под которыми толщина пленки удовлетворяет условию максимума (16.6). Эти полосы называются полосами равной толщины. В случае если на пленку падает белый свет, то полосы будут иметь
радужную окраску.А теперь вспомните, как переливаются всеми цветами радуги мыльные пузыри, бензиновые пленки на поверхности воды в речном порту или на асфальте после дождя. Объясните эти явления.
Интерференционная картина возникает при отражении света от стеклянной пластины и положенной на нее плосковыпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны R (рис.16.11). В этом случае накладываются лучи 1 и 2, отраженные от двух границ тонкой прослойки воздуха между линзой и пластинкой. В случае если толщина воздушной прослойки d удовлетворяет условию максимума (16.6), то лучи при интерференции усиливают друг друга, на расстоянии rk от оси симметрии возникает светлое пятно. Ясно, что все светлые пятна, под которыми толщина воздушной прослойки равна d, находятся на окружности радиуса rk и образуют в отраженном свете светлое кольцо радиуса rk . Таких светлых колец будет много, каждому из них соответствует различные толщины воздушного зазора, при которых выполняется условие максимума (16.6). Эти кольца являются полосами равной толщины и получили название колец Ньютона.
Радиусы колец Ньютона зависят от длины волны света λ0 , показателя преломления n среды, заполняющей зазор (для воздуха n =1), от радиуса кривизны R линзы и от номера k кольца:
, k = 1, 2, 3, …. (16.9)
В белом свете кольца Ньютона имеют радужную окраску. Кольца Ньютона наблюдаются и в проходящем свете. Попробуйте на рисунке 16.11 показать лучи 1 и 2, которые интерферируют в проходящем свете.
oplib.ru
Лабораторная работа № 5.0 экспериментальное изучение интерференции света в тонких пленках – кольца ньютона.
Задание:
изучить явление интерференции света в тонких пленках;
проанализировать изменение характера интерференционной картины в зависимости от длины волны;
определить радиус кривизны линзы.
Приборы и оборудование: экспериментальная установка, включающая в себя микроскоп, плоскопараллельную пластинку, плосковыпуклую линзу, источник света (набор светодиодов на разные длины волн).
Элементы теории
Интерференция волн – сложение в пространстве двух (или нескольких) волн, при котором в разных его точках получается усиление или ослабление результирующей волны в зависимости от разности фаз складываемых волн.
Интерференционная картина характерна для волн любой природы: волн на поверхности жидкости, упругих (например, звуковых), электромагнитных (например, радиоволн или световых). Устойчивая во времени и достаточно контрастная интерференционная картина наблюдается при соблюдении ряда условий: сдвиг фаз колебаний источников волн должен оставаться неизменным с течением времени, направления колебаний в интерферирующих волнах должны быть одинаковыми, а частоты колебаний равны. Перечисленные условия называются условиями когерентности волн.
Когерентность – это согласованное протекание во времена нескольких колебаний или волновых процессов, которое выражается в постоянстве или закономерной связи между направлениями колебаний, их фазами, частотами и амплитудами. Колебания называются когерентными, если разность их фаз остается постоянной величиной.
Интерферировать между собой могут только когерентные волны. Источники излучений, испускающие волны такого типа называются когерентными.
Интерференция света – явление, возникающее при наложении двух или нескольких когерентных световых волн– частный случай общего явления интерференции волн.
Монохроматическая волна – это синусоидальная волна с постоянными во времени частотой, амплитудой и начальной фазой. Колебания, возбуждаемые в любой точке пространства такой волной, будут длиться бесконечно долго. Поэтому монохроматические колебания и волны являются когерентными.
Рассмотрим две монохроматические световые волны, которые имеют одну и ту же частоту.
Напряженности электрического поля этих волн описываются уравнениями
(1)
где А1 иА2 – амплитуды колебаний напряженностей электрического поля, ω – частота колебаний, - волновой вектор, указывающий направление распространение волны,
- волновой вектор, указывающий направление распространение волны,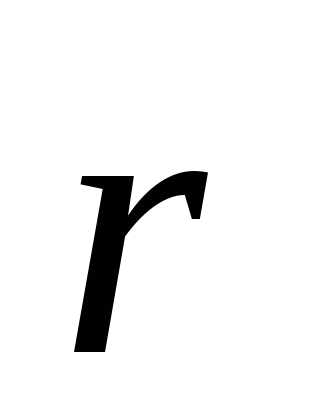 радиус-вектор, проведенный в рассматриваемую точку,α1 иα2 - начальные фазы колебаний.
радиус-вектор, проведенный в рассматриваемую точку,α1 иα2 - начальные фазы колебаний.
В некоторой точке Ррезультирующее электрическое поле будет определяться векторной суммой полей
(2)
и, следовательно,
(3)
При совпадении направлений колебаний вектора  в складывающихся волнах и при неизменной разности фазинтерферирующих волн интенсивность в точкеР определяется уравнением
в складывающихся волнах и при неизменной разности фазинтерферирующих волн интенсивность в точкеР определяется уравнением
. (4)
Максимумы интенсивности определяются выражением
(5)
и соответствуют значениям 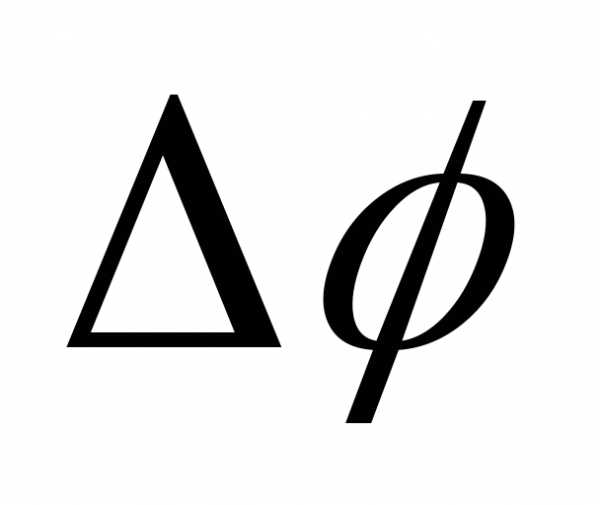 , равным 0, 2
, равным 0, 2 , 4
, 4 , … т.е.
, … т.е.
, m= 0, 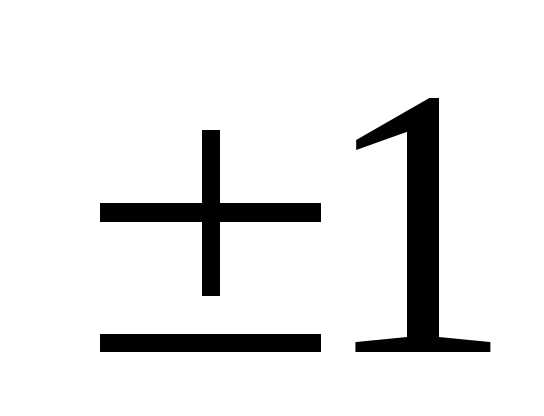 ,
,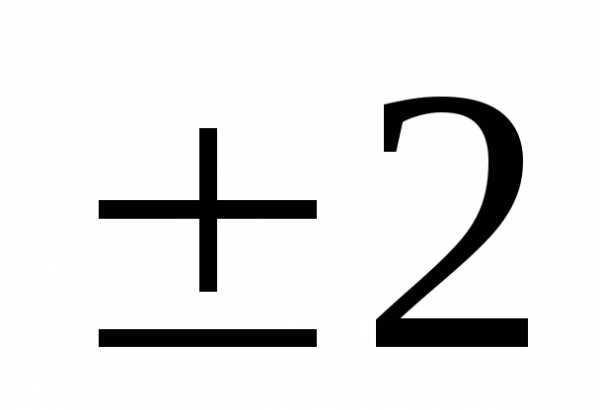 , … (6)
, … (6)
Минимумы интенсивности определяются выражением
(7)
и соответствуют значениям 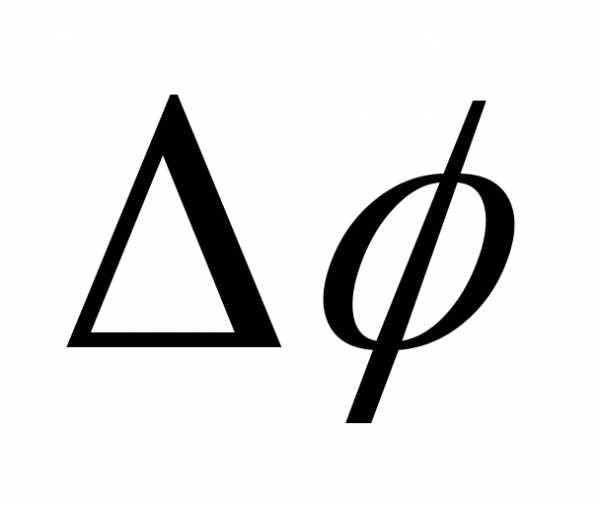 , равным
, равным , 3
, 3 , 5
, 5 , … т.е.
, … т.е.
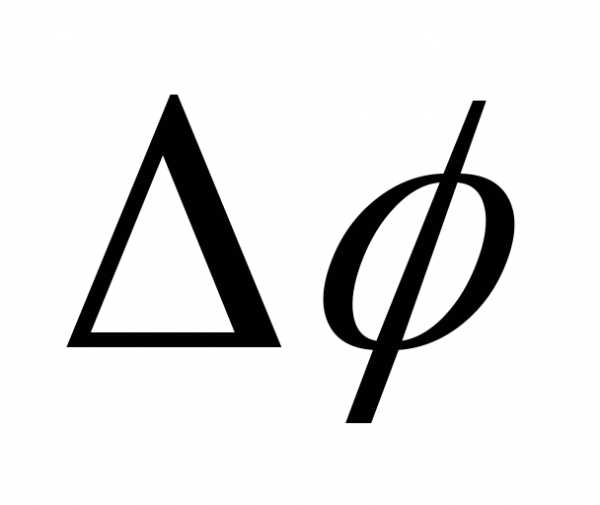 =(2m+1),m= 0,1,2, … (8)
=(2m+1),m= 0,1,2, … (8)
В частном случае при 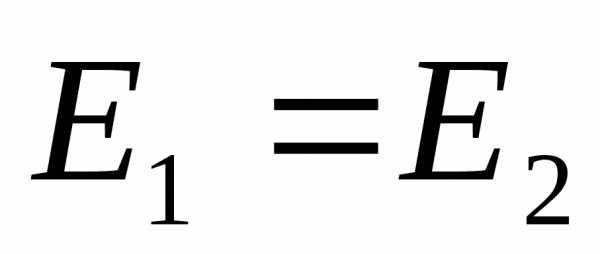 соотношение (4) имеет вид
соотношение (4) имеет вид
. (9)
В зависимости от значений 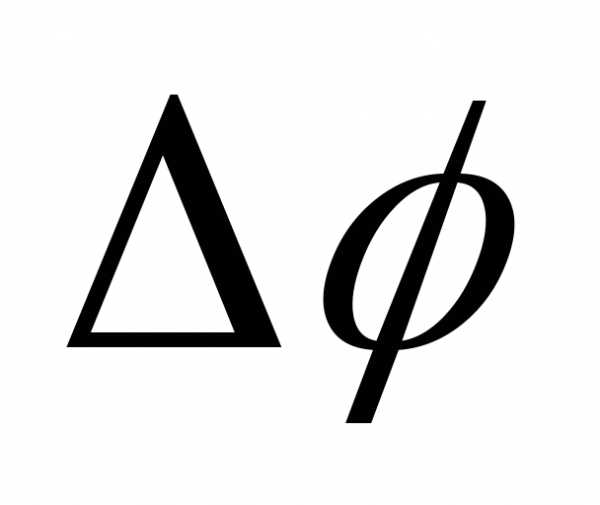 интенсивность изменяется от минимального значения
интенсивность изменяется от минимального значения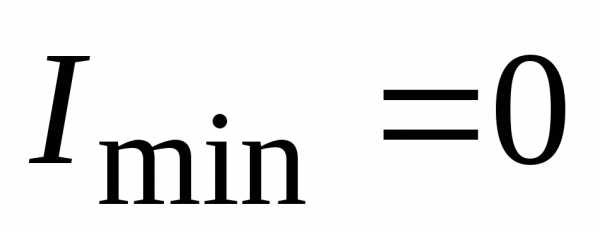 до максимального значения
до максимального значения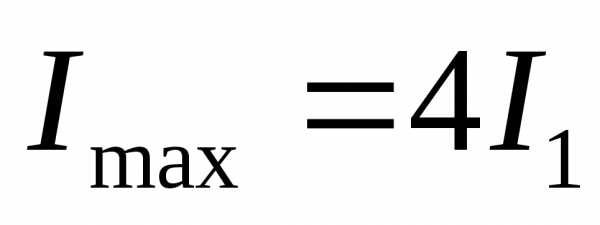 .
.
Таким образом, при суперпозиции волн соотношение между их амплитудами существенно сказывается на качестве интерференционной картины. Результат интерференции определяется разностью фаз интерферирующих волн в точке наблюдения, т.е. зависит от начальной разности фаз 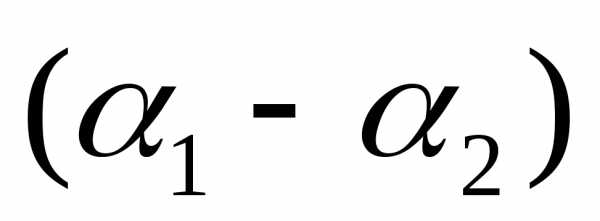 и от разности расстояний
и от разности расстояний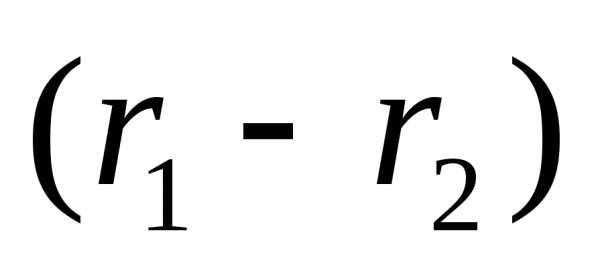 , геометрической разности хода. Для когерентных волн начальная разность фаз постоянна и, следовательно, интенсивность света в разных точках пространства зависит только от разности расстояний
, геометрической разности хода. Для когерентных волн начальная разность фаз постоянна и, следовательно, интенсивность света в разных точках пространства зависит только от разности расстояний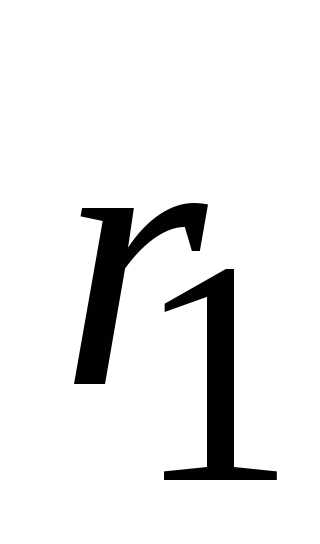 и
и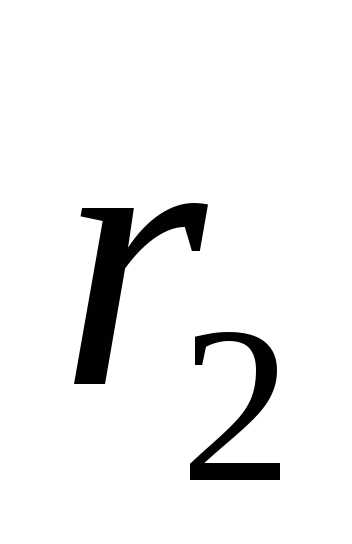 .
.
Разность фаз в данном случае определяется уравнением
, (10)
т.к. 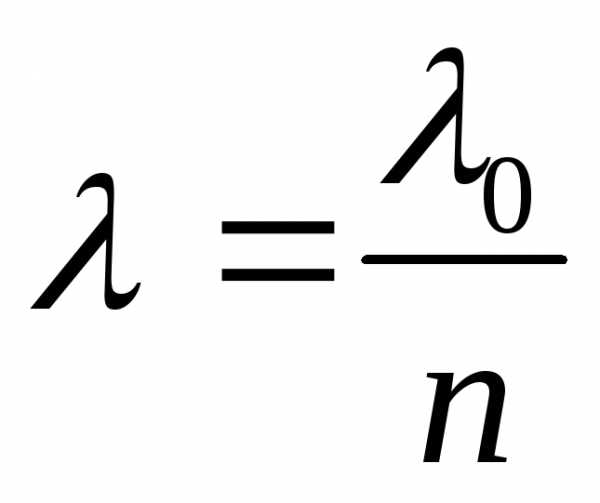 , где
, где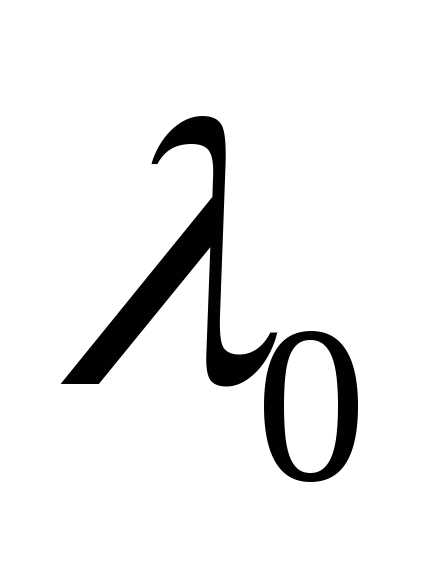 - длина световой волны в вакууме,n– абсолютный показатель преломления среды.
- длина световой волны в вакууме,n– абсолютный показатель преломления среды.
Произведение показателя преломления на длину пути 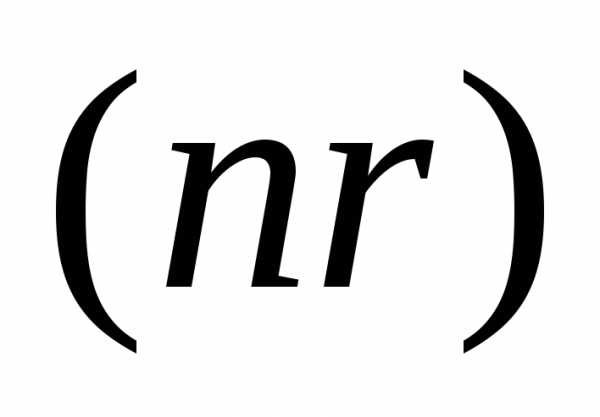 называетсяоптической длиной пути, а величина, равная разности оптических длин путей, проходимых волнами, называетсяоптической разностью хода.
называетсяоптической длиной пути, а величина, равная разности оптических длин путей, проходимых волнами, называетсяоптической разностью хода.
Обозначив оптическую разность хода через , получим
, получим
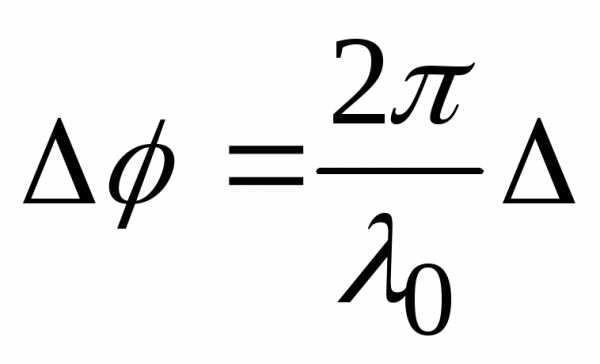 . (11)
. (11)
Формула (11) выражает связь разности хода и разности фаз.
Если оптическая разность хода равна целому числу длин волн (четному числу полуволн длин волн, в вакууме), т.е если , то разность фаз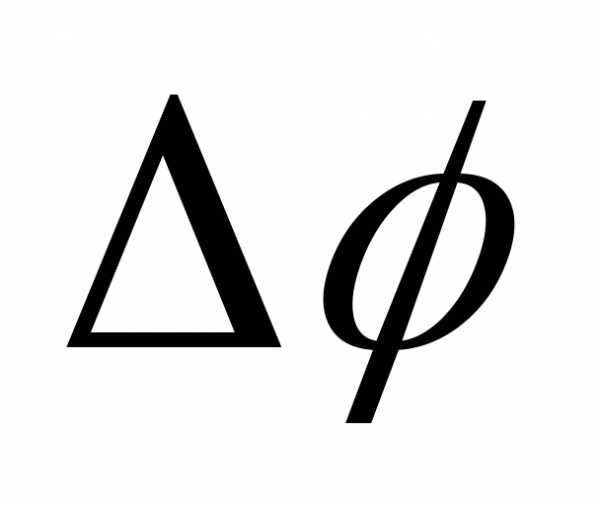 оказывается кратной
оказывается кратной и колебания, возбуждаемые в точкеРобеими волнами, будут синфазными. Таким образом, считая, интерференционный максимум наблюдается при
и колебания, возбуждаемые в точкеРобеими волнами, будут синфазными. Таким образом, считая, интерференционный максимум наблюдается при
, (12)
где m= 0, 1, 2, … – порядок интерференции.
Если оптическая разность хода равна полуцелому числу длин волн, то колебания в точке Рнаходятся в противофазе. Следовательно, интерференционный минимум наблюдается при
, (13)
или
, (m= 0, 1, 2, …).
Область пространства, в которой волны от когерентных источников перекрываются, называется полем интерференции. В этой области наблюдается чередование максимумов и минимумов. Предельный порядок интерференции определяется условием
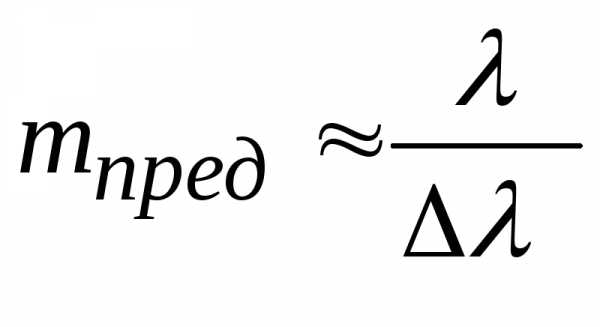 , (14)
, (14)
где 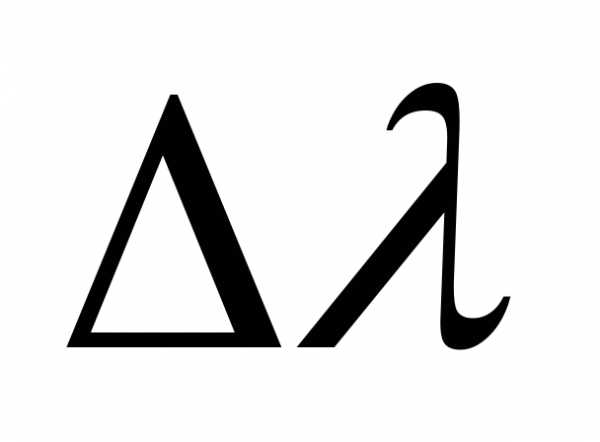 – ширина спектра излучения.
– ширина спектра излучения.
Из выражения (14) следует, что контрастность интерференционной картины уменьшается тем быстрее, чем шире спектр излучения. При освещении, например, белым светом интерференционные полосы для лучей с близкими длинами волн частично перекрываются, в результате чего общая картина «расплывается». В центре экрана (m= 0) максимумы для всех длин волн совпадают и получается белая полоса, слегка красноватая по краям. Спектр первого порядка (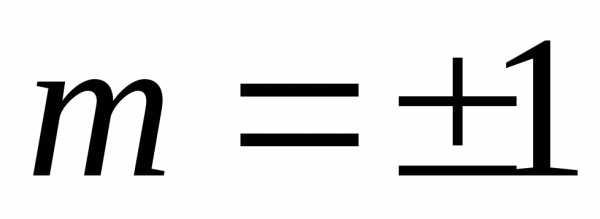 ) будет иметь радужную окраску, а интерференционные спектры более высоких порядков могут перекрываться, поскольку максимумы более коротких длин волн будут попадать в те же места, что и максимумы более длинных волн в спектрах других порядков.
) будет иметь радужную окраску, а интерференционные спектры более высоких порядков могут перекрываться, поскольку максимумы более коротких длин волн будут попадать в те же места, что и максимумы более длинных волн в спектрах других порядков.
Практически единственной возможностью заметить интерференцию света в обыденной жизни является наблюдение цветных пятен в тонких пленках масла, бензина и т.п., разлитых на поверхности воды. Бесформенность пятен объясняется различием и непостоянством толщины пленки, а разноцветность – наличием в белом свете различных длин волн.
Интерференция в тонких пленках широко используется в современной технике для просветления оптических поверхностей, ликвидации «бликов» от поверхностей линз, получения интерференционных фильтров.
Полосы, возникающие при интерференции света в тонких пленках, толщина которых неодинакова в разных местах, получили название полос равной толщины. Классическим примером полос равной толщины являются кольца Ньютона. Их можно наблюдать от тонкой клиновидной прослойки, образованной параллельной пластинкой и соприкасающейся с ней выпуклой линзой с большим радиусом кривизны поверхности (рис. 1).
Рис.1. Рис.2.
Радиусы интерференционных колец 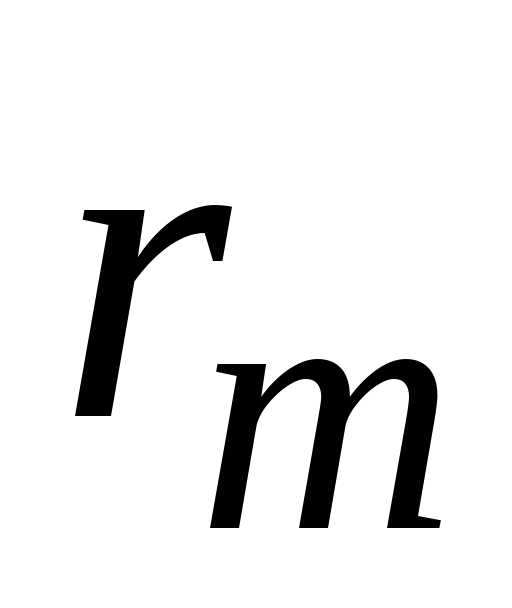 зависят от радиуса кривизны линзы: ширина и интенсивность колец убывает по мере удаления от центрального пятна. Полосы равной толщины локализованы вблизи воздушной прослойки, а наблюдение ведется с помощью микроскопа, сфокусированного на поверхность пластинки.
зависят от радиуса кривизны линзы: ширина и интенсивность колец убывает по мере удаления от центрального пятна. Полосы равной толщины локализованы вблизи воздушной прослойки, а наблюдение ведется с помощью микроскопа, сфокусированного на поверхность пластинки.
Допустим, что линза освещается источником монохроматического света (рис 2., луч 1; рис. 2 является фрагментом рисунка 1). Световые волны в точке Аразделяются на два пучка, частично отражаясь от нижней поверхности линзы (луч 2) и частично от плоскопараллельной пластинки (луч 3). Волны, отраженные в точкахАиВ, интерферируют между собой.
Ввиду малости кривизны поверхности линзы и при нормальном падении света на линзу точки АиСнаходятся на малом расстоянии друг от друга. Тогда оптическая разность хода интерферирующих лучей 2 и 3 будет равна удвоенной оптической толщине между линзой и пластинкой, сложенной с дополнительной разностью хода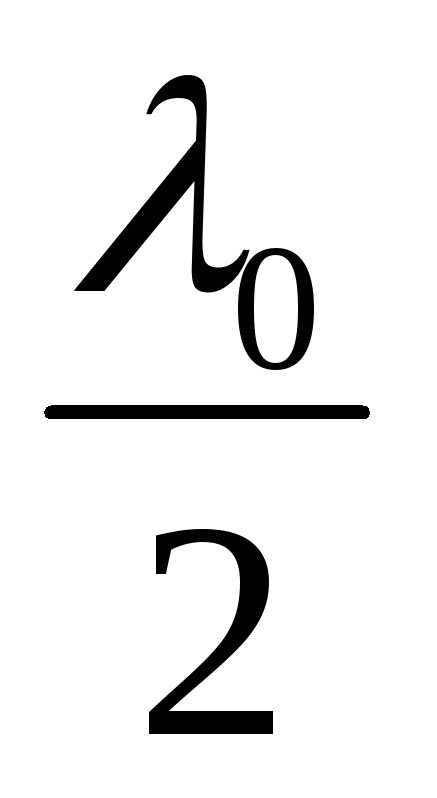 , которая возникает при отражении луча от оптически более плотной среды в точкеВ:
, которая возникает при отражении луча от оптически более плотной среды в точкеВ:
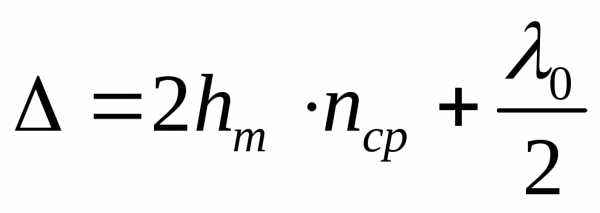 . (15)
. (15)
Минимум интенсивности для воздушного зазора hm (nср = 1) определяется из условия
, (16)
т.е.
. (17)
В соответствии с рис. 1
, (18)
или , (19)
где R– радиус кривизны линзы, величина, постоянная для данной линзы.
Так как 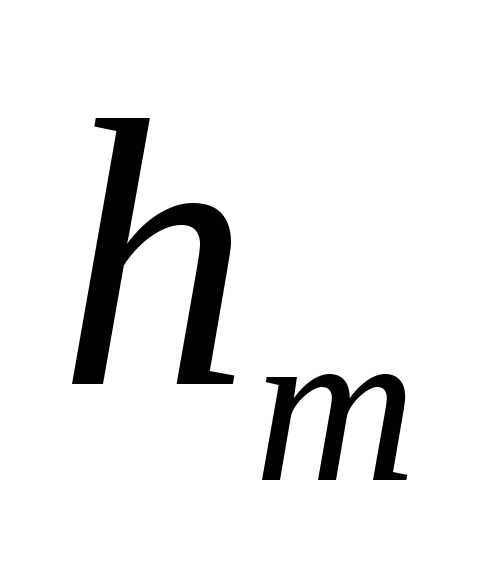 R, то
R, то
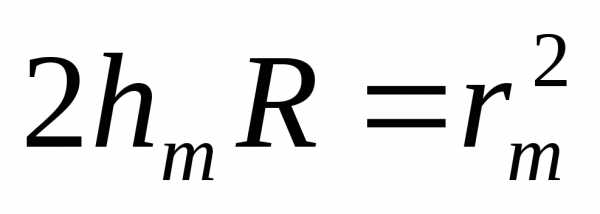 . (20)
. (20)
Тогда с учетом (17) радиус темного кольца
. (21)
Максимумы интенсивности будут наблюдаться при условии
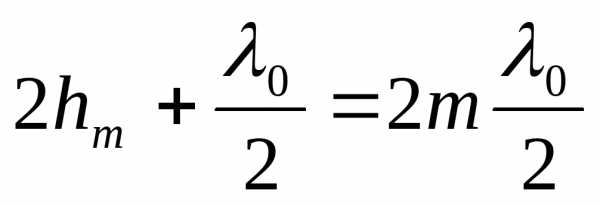 , (22)
, (22)
а радиус светлого кольца с учетом (20) и (22)
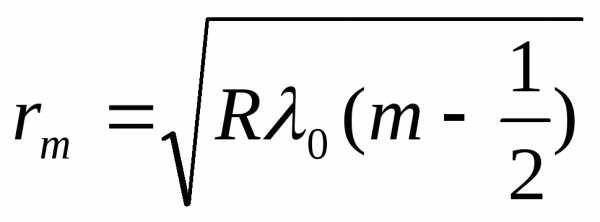 . (23)
. (23)
Чем больше m, тем меньше различие между радиусами соседних колец, тем уже кольца. Значениюm= 0 соответствует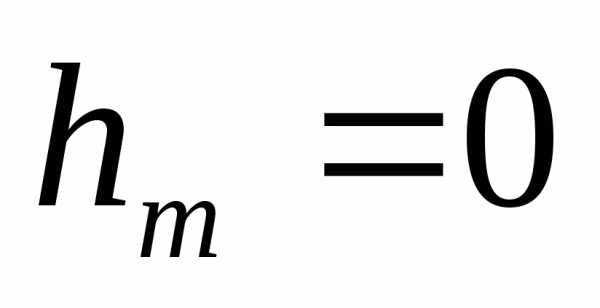 , т.е. точка в месте касания пластинки и линзы. В этой точке наблюдается минимум интенсивности. Вследствие упругой деформации стекла невозможно добиться соприкосновения сферической поверхности линзы и пластинки строго в данной точке, поэтому центральное пятно имеет конечные размеры.
, т.е. точка в месте касания пластинки и линзы. В этой точке наблюдается минимум интенсивности. Вследствие упругой деформации стекла невозможно добиться соприкосновения сферической поверхности линзы и пластинки строго в данной точке, поэтому центральное пятно имеет конечные размеры.
Как следует из (16) и (17), при переходе от одного темного пятна к другому разность хода Δhизменяется на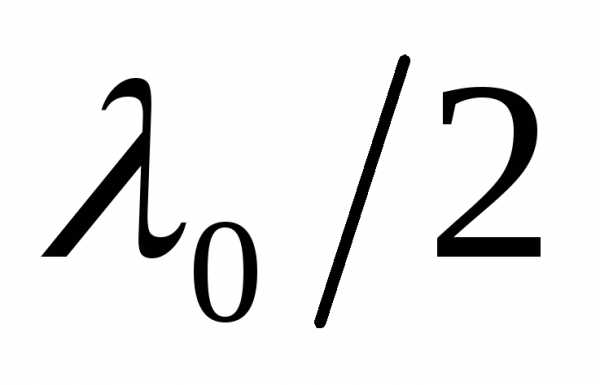 . При переходе отn-го кольца к
. При переходе отn-го кольца к
m-му оптическая толщина воздушного зазора возрастает на:
. (24)
Учитывая (20) и (24), получаем
, (25)
откуда радиус кривизны линзы
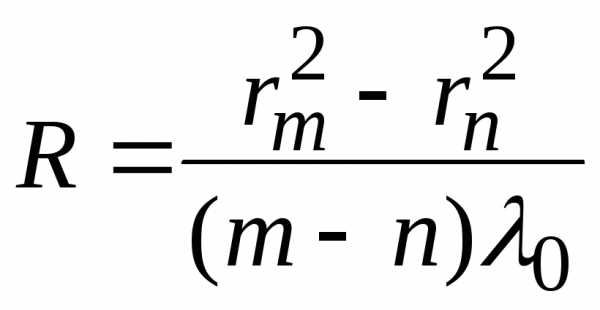 . (26)
. (26)
С помощью установки, пользуясь формулой (26), при известном значенииRможно определять длины волн падающего излучения. Для заданных значенийRиλ0на основе выражений (21) и (23) можно определить радиусы соответственно темных и светлых колец. Наконец, зная длину волныλ0, можно рассчитать величину зазораhm.
studfiles.net
Интерференция в тонких плёнках
При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от верхней и нижней поверхности плёнок (рис. 4.16). Для белого света, представляющего собой смешение электромагнитных волн из всего оптического спектра интерференционные полосы приобретают окраску. Это явление получило название цветов тонких плёнок. Цвета тонких плёнок наблюдаются на стенках мыльных пузырьков, на плёнках масла, нефти, на поверхности металлов при их закалке (цвета побежалости).
Для объяснения этих явлений рассмотрим расположенную в вакууме плоско параллельную диэлектрическую пластинку (рис.) толщины с показателем преломления , где - диэлектрическая проницаемость диэлектрика освещаемую плоской световой монохроматической волной с длиной волны под углом (рис. 4.16). При отражении световых волн от верхней и нижней поверхности пластинки между отражёнными волнами возникнет оптическая разность хода , которая является следствием того факта, что волна, отражённая от нижней поверхности пластинки проходит больший путь внутри диэлектрической пластинки, чем
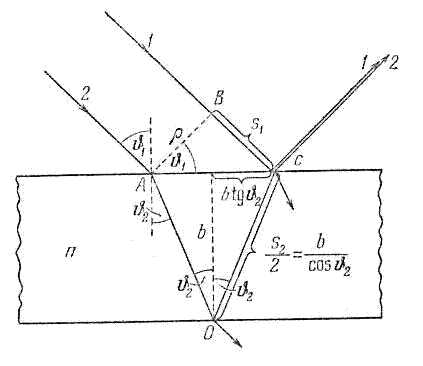 |
| Рис. 4.16. |
волна, отражённая от верней поверхности в вакууме, приобретающая дополнительный набег фазы при отражении от оптически более плотной среды. Из геометрических соображений следует, что:
| , | (4.23) |
где - угол преломления падающего светового пучка пластинкой (рис. 4.16), связанного с углом падения соотношением следующим из закона Снеллиуса: .
При условии, что
| (4.24a) |
кратно целому числу ... длин волн, в точке наблюдения на расстоянии от поверхности плёнки во много раз большем, чем толщина пластинки, отражённые от обеих поверхностей пластинки волны будут складываться в фазе и формировать интерференционный максимум.
Аналогичным образом получим условия минимума интерференционной картины в точке наблюдения на бесконечности, если волны отражённые от обеих поверхностей пластинки волны будут складываться в противофазе, т.е.
| , | (4.24b) |
где произвольное целое число.
Интерференционная картина, образованная отражёнными под разными углами плоскими волнами от поверхностей плоско параллельной пластинки / плёнки, получила название интерференционных полос равного наклона. В этом названии отражается тот факт, наблюдаемая интерференционная картина образована параллельно распространяющимися волнами, падающими на пластинку под одним углом / наклоном. Область наблюдения интерференции расположена в бесконечности, где "пересекаются" параллельные лучи. Углы, в направлении которых формируются максимумы и минимумы интерференционной картины в соответствии с (4.24) зависят от длины волны. Это объясняет окраску интерференционной картины световых лучей, отражённых от поверхностей плоско параллельной пластинки при её облучении белым светом.
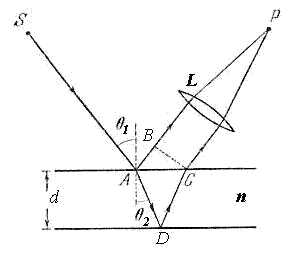 |
| Рис. 4.17. |
Для наблюдения интерференционной картины полос равного наклона на конечном расстоянии от пластинки используется линза (рис. 4.17). Благодаря свойству линзы параллельные световые лучи сходятся в некоторой точке фокальной плоскости. Эта точка совпадает с фокусом линзы, если лучи параллельны главной оптической оси. В силу зависимости (4.24) направления на главные максимумы и минимумы от длины волны, в фокальной плоскости линзы можно наблюдать окрашенную в цвета оптического спектра интерференционную картину полос равного наклона.
Другой вид интерференции света в тонких плёнках, толщина которых меняется её по поперечному сечению, получил название интерференционных полос равной толщины. Для изучения этого явления рассмотрим плёнку переменной толщины в виде клина (рис. 4.18). Рассмотрим падающую на поверхность диэлектрического клина с показателем преломления , где - диэлектрическая проницаемость диэлектрика, плоскую световую монохроматическую волну I с длиной волны (рис. 4.18).
Отражённые от верхней и нижней граней клина плоские волны I' и I" (рис. 4.18) пересекутся вблизи поверхности клина из-за не параллельности его граней . Следовательно, при помещении экрана вблизи поверхности клина можно наблюдать интерференционную картину в виде полос, параллельных ребру клина, которую образуют волны, отразившиеся от его граней в тех точках их поверхности, где клин имеет одинаковую толщину. Это объясняет названия рассматриваемого явления. При облучении поверхности клина белым светом интерференционная картина в виде полос равной толщины оказывается окрашенной в цвета оптического спектра. Для наблюдения интерференционной картины в виде полос равной толщины используется линза (рис. 4.19), назначение которой состоит в увеличении изображения интерференционной картины, для её визуального наблюдения.
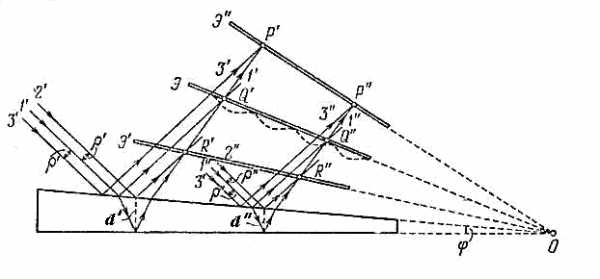 |
| Рис. 4.18. |
Интерференционная картина в виде полос равной толщины широко используется на практике для контроля степени неровности различных поверхностей, плёнок, а также всевозможных покрытий. Если поверхности плёнки неровные, то полосы равной толщины принимают неправильную причудливую форму, связанную с соответствующим контуром равной толщины плёнки.
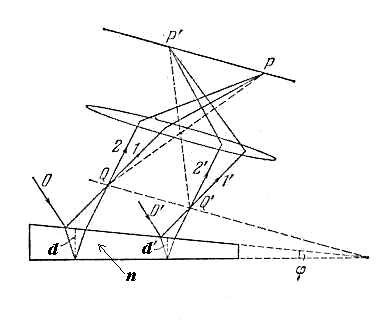 |
| Рис. 4.19. |
Для получения количественных соотношений, характерных для рассматриваемого явления , рассмотрим расчёт интерференционной картины в виде колец Ньютона, которая имеет место при освещении плоской монохроматической световой волной с длиной волны диэлектрической (стеклянной) линзы (рис. 4.20) с показателем преломления диэлектрика , помещённой на отражающую поверхность (зеркало).
Найдём оптическую разность хода волн, отражённых от нижней поверхности линзы и от поверхности зеркала. Для облегчения расчётов заменим внутреннюю криволинейную поверхность линзы в точке отражения луча плоскостью, параллельной отражающей поверхности (рис. 4.20). В результате такого упрощения удаётся свести расчёт интерференционной картины в виде колец Ньютона к расчёту интерференционной картины в виде полос равной толщины. Полосы представляют собой концентрические эллипсы при наклонном падении света на линзу или окружности при нормальном падении. Как следует из приведенных выше рассуждений о возможности наблюдения полос равной толщины, соответствующая интерференционная картина наблюдается вблизи поверхности плёнки. В первом приближении можно полагать, что наблюдаемые интерференционные полосы располагаются непосредственно на поверхности плёнки в точке отражения волны. Тогда радиусы колец Ньютона (рис. 4.20) равны
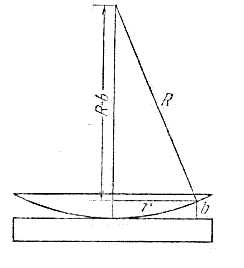 |
| Рис. 4.20. |
радиусам окружностей, каждая из которых соответствует точкам нижней поверхности линзы, находящихся на одинаковом расстоянии от отражающей поверхности. Если предположить, что - радиус кривизны линзы, а , то (рис. 4.20)
| (4.25a) |
| . | (4.25b) |
Радиусы колец Ньютона , соответствующих интерференционным максимумам с номерами , получающихся при нормальном падении световой волны к поверхности пластинки можно найти из (4.24a)при и с учётом (4.24b):
| , | (4.26) |
где - длина световой волны, освещающей линзу.
Чётным значениям соответствуют светлые кольца, а нечётным - тёмные (рис. 4.21). В частности в центре картины будет находиться тёмное кольцо, вырождающееся в тёмную точку и соответствующее направлению противофазного сложения интерферирующих волн. Если линзу при наблюдении колец Ньютона поднимать вертикально вверх, то из-за
 |
| Рис. 4.21. |
увеличения проходимого лучами пути интерференционные кольца, каждое из которых соответствует некоторой постоянной разности хода, будет стягиваться к центру. При этом центр картины по мере поднятия линзы будет становиться попеременно то светлым, то тёмным.
stydopedia.ru
8. Интерференция света методом колец Ньютона
а
б
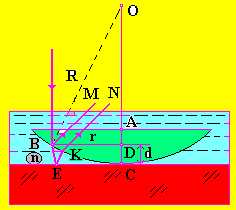
Рис. 9
Полосы равной толщины можно наблюдать с помощью установки «Кольца Ньютона» (рис. 9, а).Установка состоит из плоско-выпуклой стеклянной линзы с радиусом кривизны R, которая выпуклой частью опирается на плоскопараллельную стеклянную пластинку.
Пространство между линзой и пластинкой может быть заполнено жидкостью с абсолютным показателем преломления n (например, для воды n=1,33).
Если на плоскую поверхность линзы падает нормально (перпендикулярно) плоская волна монохроматического света, то в точке В (r = ВD) свет частично преломляется (луч ВЕ) и отражается от верхней (луч ВМ) и нижней (луч ЕК) поверхностей клина между линзой и пластинкой.
Оптическая разность хода между этими отраженными лучами
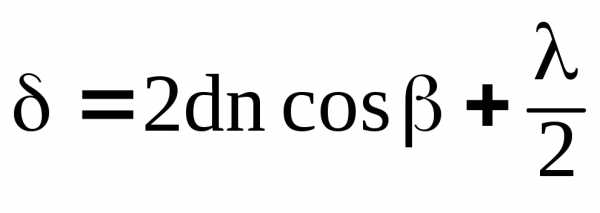 (20)
(20)
или 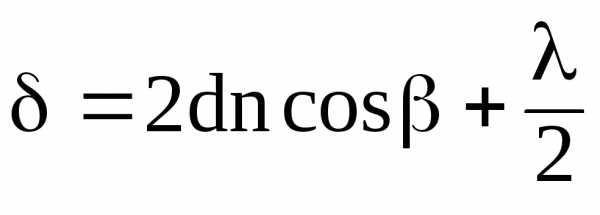 , (21)
, (21)
т. е. 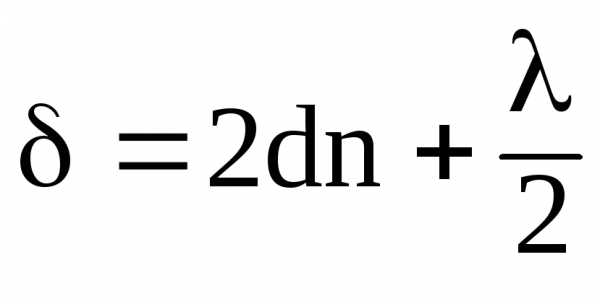 , (22)
, (22)
где cos = 1, т. к. = = 00.
Здесь учтено, что при отражении света от стекла
nст > nж= n
происходит сдвиг по фазе на , т. е. появляется дополнительная разность хода 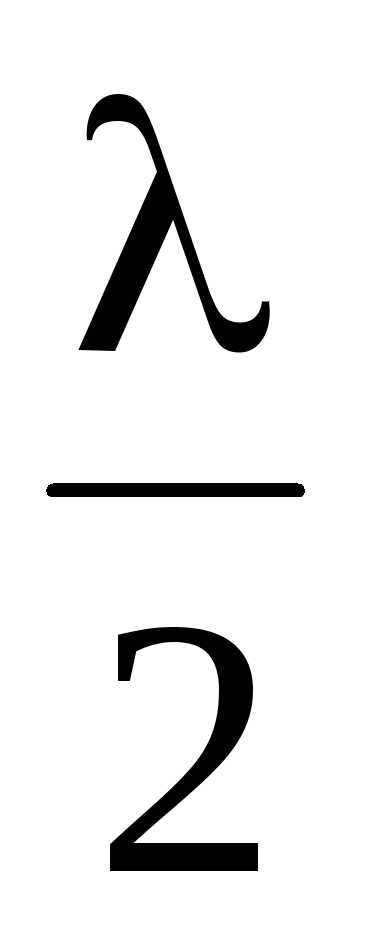 . Из-за невозможности непосредственного измерения величины d, рассмотрим треугольник ОВD,
. Из-за невозможности непосредственного измерения величины d, рассмотрим треугольник ОВD,
где
R2 = r2 + OD2,
но OD = R d,
т. е.
r2 =2Rd (23)
(d << R и cлагаемым d2 можно пренебречь).
Следовательно,
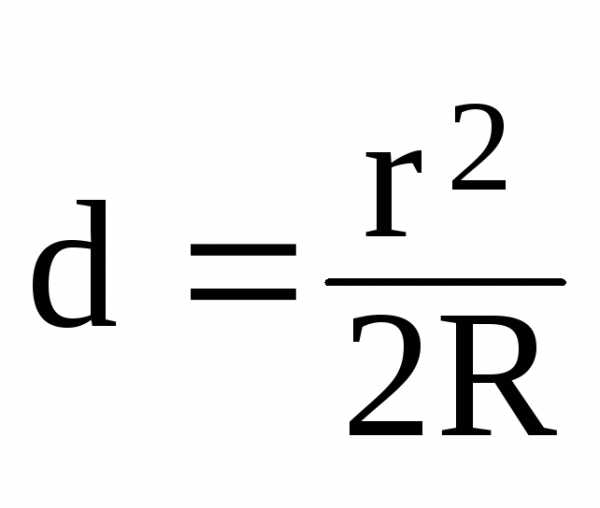 . (24)
. (24)
С учетом (24) оптическую разность хода запишем в виде
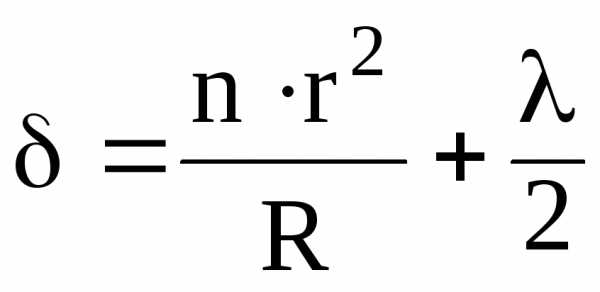 .
.
При
мах = 2m
максимум интерференции на отражение удовлетворяет условию
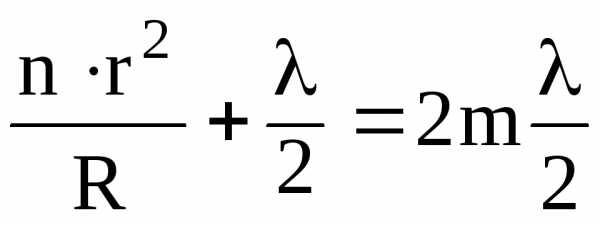 ,
,
где m = 1, 2, 3, …, - порядок интерференции.
или 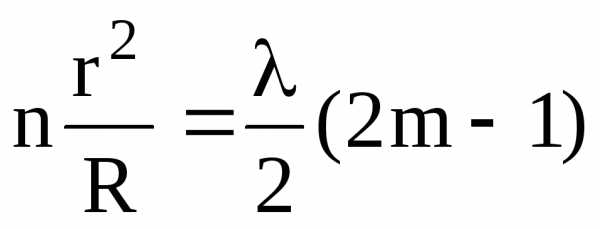 .
.
Радиус светлого кольца на отражение
. (25)
При min = (2m +1)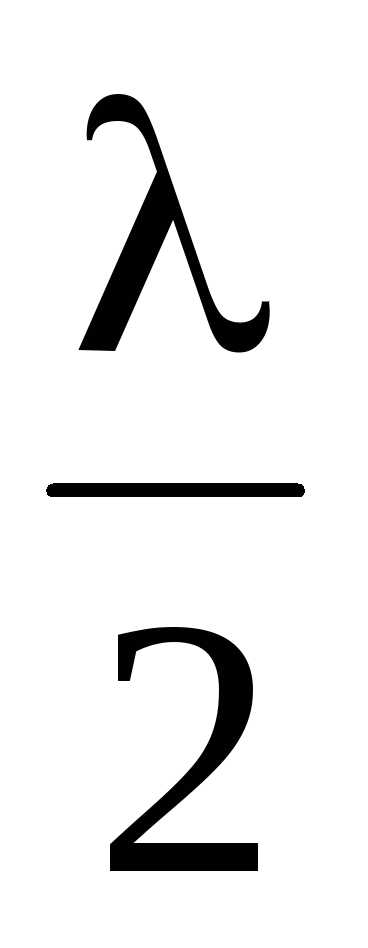 (минимум интерференции на отражение) радиус темного кольца
(минимум интерференции на отражение) радиус темного кольца
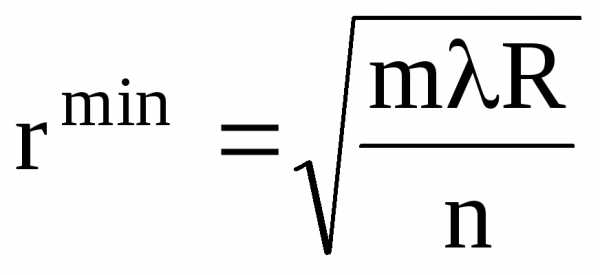 . (26)
. (26)
Аналогичный расчет можно провести для интерференции на просвет.
Таким образом, при сложении отраженных волн от поверхностей клина возникают интерференционные кольца равной толщины. В центре находится темное пятно (минимум), которое окружено системой концентрических светлых (максимум) и темных колец, ширина и интенсивность которых постепенно убывают по мере удаления от центра (рис. 9, б).
Так как центральное пятно в отраженном свете темное, а в проходящем светлое, следовательно, при отражении света от среды с большим показателем преломления, фаза отраженной волны меняется на . А при отражении от среды с меньшим показателем преломления изменение фазы не происходит. Это подтверждается специальным опытом Юнга.
К пластинке из флинта (n = 1,7) прижимают линзу из крона (n = 1,5), а пространство между ними заполняют сассафрасовым маслом с промежуточным показателем преломления. В этом случае фаза волны менялась на при отражении как от верхней, так и от нижней поверхностей масляной прослойки. Поэтому в центре наблюдается максимум (светлое пятно) в отраженном и минимум (темное пятно) в проходящем свете.
studfiles.net
3.Метод наблюдения интерференции. Кольца Ньютона. Интерференция в тонких пленках. Расчет интерференционной картины. Просветление оптики. Интерферометр Майкельсона.
Главная » Самолетостроение » Физика (3 семестр) » 3.Метод наблюдения интерференции. Кольца Ньютона. Интерференция в тонких пленках. Расчет интерференционной картины. Просветление оптики. Интерферометр Майкельсона.3.Метод наблюдения интерференции. Кольца Ньютона. Интерференция в тонких пленках. Расчет интерференционной картины. Просветление оптики. Интерферометр Майкельсона.
Для осуществления интерференции света необходимо получить когерентные световые пучки, для чего применяются различные приемы. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.
1. Метод Юнга. Источником света служит ярко освещенная щель S (рис. 245), от которой световая волна падает на две узкие равноудаленные щели S1 и S2, параллельные щели S. Таким образом, щели S1 и S2 играют роль когерентных источников.
Интерференционная картина (область ВС) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S1 и S2. Как уже указывалось (см. § 171), Т. Юнгу принадлежит первое наблюдение явления интерференции.
2. Зеркала Френеля. Свет от источника S (рис. 246) падает расходящимся пучком на два плоских зеркала А1О и А2О, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол j мал). Используя правила построения изображения в плоских зеркалах, можно показать, что и источник, и его изображения S1 и S2 (угловое расстояние между которыми равно 2j) лежат на одной и той же окружности радиуса r с центром в О (точка соприкосновения зеркал).
Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S1 и S2, являющихся мнимыми изображениями S в зеркалах. Мнимые источники S1 и S2 взаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рис. 246 она заштрихована). Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше 2j. Интерференционная картина наблюдается на экране (Э), защищенном от прямого попадания света заслонкой (З).
3. Бипризма Френеля. Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S (рис. 247) преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S1 и S2, являющихся когерентными. Таким образом, на поверхности экрана (в заштрихованной области) происходит наложение когерентных пучков и наблюдается интерференция.
Расчет интерференционной картины от двух источников. Расчет интерференционной картины для рассмотренных выше методов наблюдения интерференции света можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу (рис. 248). Щели S1 и S2 находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми изображениями источника S в какой-то оптической системе) источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей.
Максимумы интенсивности будут наблюдаться в случае, если
а минимумы — в случае, если
Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно
Dx не зависит от порядка интерференции (величины т) и является постоянной для данных l, d и l0.
Кольца Ньютона. Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падения света имеющие вид концентрических окружностей.
В отраженном свете оптическая разность хода (с учетом потери полуволны при отражении), согласно (174.1), при условии, что показатель преломления воздуха n=1, а i=0, где d—ширина зазора. Из рис. 252 следует, что , где R—радиус кривизны линзы, r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим d=r2/(2R). Следовательно,
Приравняв к условиям максимума и минимума получим выражения для радиусов m-го светлого кольца и m-го темного кольца соответственно
Измеряя радиусы соответствующих колец, можно (зная радиус кривизны линзы R) определить l0 и, наоборот, по известной l0 найти радиус кривизны R линзы.
Интерференция в тонких пленках. В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленка на металлах), возникающее в результате интерференции света, отраженного двумя поверхностями пленки.
Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом i (рис. 249) падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, а частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (п0=1), а частично отразится и пойдет к точке В. Здесь он опять частично отразится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом i. Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их пути поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы. В результате возникает интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами.
В точке Р будет интерференционный максимум, если
и минимум, если
Интерференция, как известно, наблюдается, только если удвоенная толщина пластинки меньше длины когерентности падающей волны.
Просветление оптики.
Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий.
Так как nс, n и показатель преломления воздуха n0 удовлетворяют условиям nс >n>n0, то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (предполагаем, что свет падает нормально, т. е. i=0)
где nd — оптическая толщина пленки. Обычно принимают m=0, тогда
Таким образом, если выполняется условие (175.1) и оптическая толщина плевки равна l0/4, то в результате интерференции наблюдается гашение отраженных лучей.
Для устранения указанных недостатков осуществляют так называемое просветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления, меньшим, чем у материала линзы. При отражении света от границ раздела воздух–пленка и пленка–стекло возникает интерференция когерентных лучей 1' и 2' (рис. 253). Толщину пленки d и показатели преломления стекла nс и пленки n можно подобрать так, чтобы волны, отраженные от обеих поверхностей пленки, гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна (см. (172.3)). Расчет показывает, что амплитуды отраженных лучей равны, если
Интерферометр Майкельсона.
Явление интерференции также применяется в очень точных измерительных приборах, называемых интерферометрами. Все интерферометры основаны на одном и том же принципе и различаются лишь конструкционно. На рис. 255 представлена упрощенная схема интерферометра Майкельсона. Монохроматический свет от источника S падает под углом 45° на плоскопараллельную пластинку P1. Сторона пластинки, удаленная от S, посеребренная и полупрозрачная, разделяет луч на две части: луч 1 (отражается от посеребренного слоя) в луч 2 (проходит через него). Луч 1 отражается от зеркала M1 и, возвращаясь обратно, вновь проходит через пластинку P1 (луч 1'). Луч 2 идет к зеркалу М2, отражается от него, возвращается обратно и отражается от пластинки Р1 (луч 2'). Так как первый из лучей проходит сквозь пластинку Р1 дважды, то для компенсации возникающей разности хода на пути второго луча ставится пластинка Р2 (точно такая же, как и Р1, только не покрытая слоем серебра).
Лучи 1' и 2' когерентны; следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точки О до зеркала М1 и луча 2 от точки О до зеркала M2. При перемещении одного из зеркал на расстояние l0/4 разность хода обоих лучей увеличится на l0/2 и произойдет смена освещенности зрительного поля. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр Майкельсона для точного (порядка 10–7 м) измерения длин (измерения длины тел, длины волны света, изменения длины тела при изменении температуры (интерференционный дилатометр)).
it-iatu.ru
Интерференция в тонких пленках.
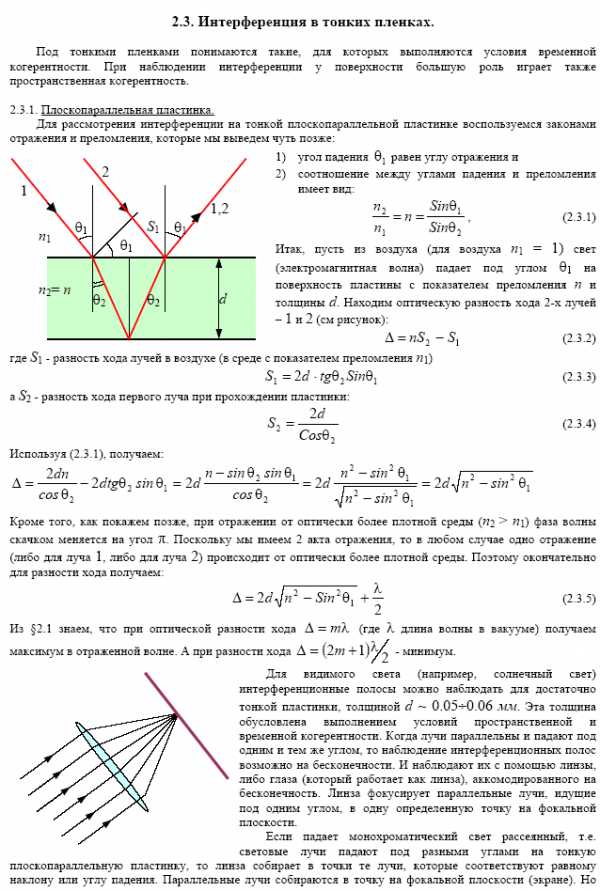


Полосы равной толщины.
Полосы равной толщины, один из эффектовоптики тонких слоев, в отличие отполос равного наклона, наблюдаются непосредственно на поверхности прозрачного слоя переменной толщины (рис. 1). Возникновение П. р. т. обусловленоинтерференцией света, отражённого от передней и задней границ слоя (П. р. т. в отражённом свете), или света, проходящего прямо через слой, с дважды отражённым на его границах (П. р. т. в проходящем свете). Полосами в строгом смысле (отчётливыми, попеременно тёмными и светлыми) обычно являются лишь П. р. т.монохроматическом светеили близком к нему (свете, длины волн которого заключены в сравнительно небольшом интервале). При этом максимумы и минимумы освещённости полос совпадают с линиями на поверхности слоя, по которымразность ходаинтерферирующих лучей одинакова и равна целому числу /2. На этих линиях одинакова геометрическая толщина слоя — отсюда название «П. р. т.». При освещениибелым светомналожение П. р. т., отвечающих лучам с разными , создаёт сложную радужно-цветовую картину, в которой П. р. т. лучей с отдельными зачастую неразличимы. П. р. т. обусловливают радужную окраску тонких плёнок (мыльных пузырей, масляных и бензиновых пятен на воде, плёнок окислов на металлах, в частностицвета побежалости, и пр.). Их используют для определения микрорельефа тонких пластинок и плёнок (рис. 2), в рядеинтерферометров и др. устройств для точных измерении (см., например,Ньютона кольцаи рис. к этой статье; кольца Ньютона — частный пример П. р. т.).
Рис. 1. Разность хода интерферирующих лучей, отражённых от верхней и нижней границ тонкого слоя, зависит от углов падения освещающих лучей. Однако разброс этих углов даже в случае протяжённых источников света обычно столь невелик, что разность хода, приобретаемая в точке М слоя лучами 1—1' и 2—2'; которые испущены разными участками (S1и S2) источника, практически одинакова. Поэтому полосы равной толщины локализованы непосредственно на поверхности слоя и их можно наблюдать без вспомогательных оптических устройств (линза на рис. может быть хрусталиком глаза). М' — точка на сетчатке глаза (или — при использовании дополнительной линзы — на экране), где фокусируется изображение точки М поверхности слоя, т. е, одной из точек линии равной толщины.
Рис. 2. Полосы равной толщины на поверхности слюдяной пластинки, характеризующие микрорельеф этой поверхности.
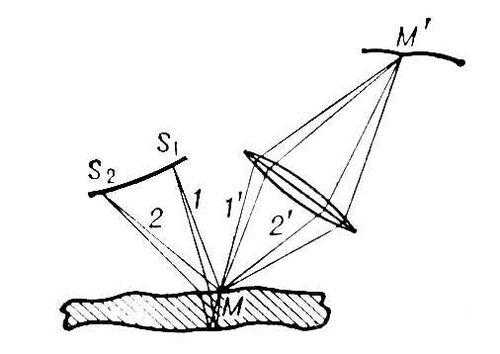

рис. 1 рис. 2
Кольца Ньютона.
Кольца Ньютона - интерференционная картина, возникающая в проходящем или отраженном свете в окрестности точки соприкосновении выпуклой поверхности с плоскостью.
После отражения лучей на границах раздела стекло-воздух и воздух стекло лучи интерферируют, образуют интерференционную картину в виде концентрических колец.
---------------------------------------------------------------------------------------------------------------------
Это оптическое явление, возникающее в тех случаях, когда в компьютер импортируется изображение с прозрачной пленки. Подобно радуге, появляющейся на поверхности мыльного пузыря, кольца появляются при плотном соприкосновении двух поверхностей, когда между ними возникает очень тонкий промежуток. Появляются, так называемые, интерференционные полосы. Чтобы избежать этого явления при сканировании прозрачных пленок, нужно класть пленку лицевой стороной прямо на стеклянную поверхность сканера.
studfiles.net
Полосы равной толщины. Кольца Ньютона.
Государственное образовательное учреждение высшего профессионального образования «Сибирский государственный медицинский университет Федерального агентства по здравоохранению и социальному развитию»
(ГОУ ВПО СибГМУ Росздрава)
Кафедра___________________________
Утверждено
На заседании кафедры
Протокол №___от « «_______2009
Ст. преподаватель Колубаева Л.А.
ЛЕКЦИЯ №7
« Интерференция на тонких пленках: полосы равного наклона и полосы равной толщины»
Томск-2009
Введение:
Интерференция на тонких пленках используется для просветления оптики и определения показателей сред и анализа их однородности.
Содержание
1. Полосы равного наклона.
2.Полосы равной толщины. Кольца Ньютона.
3.Условия наблюдения интерференции на тонких пленках
4..Просветленная оптика.
5Стоячие волны.
6.Опыт Винера, обоснование введения понятия светового вектора.
7.Интерферометр Жамена и его использование для определения показателя преломления.
8.Дифракция света. Дифракция Френеля и дифракция Фраунгофера.
9. Принцип Гюйгенса-Френеля.
Литература
1.Ландсберг Оптика
2. Савельев И.В. Курс общей физики т.3 М.изд. Дрофа,2003г.
3. .Калитиевский Н.И. Волновая оптика, М. изд. Наука1986г
4.ТрофимоваТ.И. Курс фидики, М., Высшая школа, 1997г.
Наглядные пособия
1.Компьютерные демонстрации
2.Презентации.
Другой вид интерференции света в тонких плёнках, толщина которых меняется её по поперечному сечению, получил название интерференционных полос равной толщины.
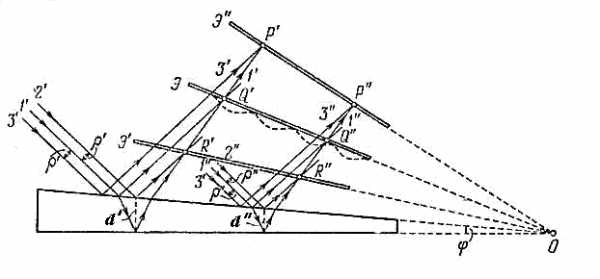
Рис.7.1
Для изучения этого явления рассмотрим плёнку переменной толщины в виде клина (рис. 7.1). Рассмотрим падающую на поверхность диэлектрического клина с показателем преломления , где- диэлектрическая проницаемость диэлектрика, плоскую световую монохроматическую волну I с длиной волны(рис. 7.1).Отражённые от верхней и нижней граней клина плоские волны I' и I" (рис. 7.1) пересекутся вблизи поверхности клина из-за не параллельности его граней . Следовательно, при помещении экрана вблизи поверхности клина можно наблюдать интерференционную картину в виде полос, параллельных ребру клина, которую образуют волны, отразившиеся от его граней в тех точках их поверхности, где клин имеет одинаковую толщину. Это объясняет названия рассматриваемого явления.
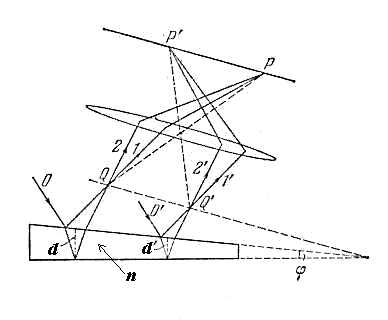
Рис.7.2
Для наблюдения интерференционной картины в виде полос равной толщины используется линза (рис. 7.2), назначение которой состоит в увеличении изображения интерференционной картины, для её визуального наблюдения.Для описания полос равной толщины можно воспользоваться следующим представлением: клин представить как совокупность полосок равной толщины, но при переходе от одной полоски к другой их толщина постепенно уменьшается (рис.7.3). Тогда разность хода между отраженными лучами от верхней и нижней граней клина будет определяться также, как для плоскопараллельных пластин:
, (7.1),где-угол преломления.
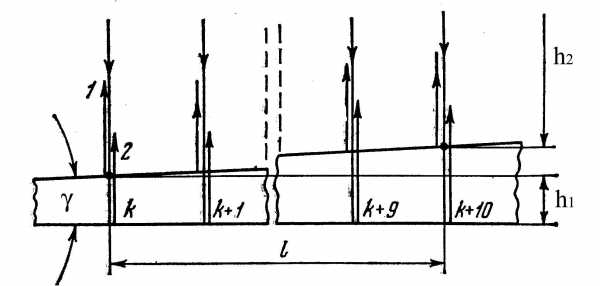
Рис.7.3
Необходимо помнить, что в выражении (7,1) /2 появляется, только тогда, когда есть точки, в которых луч отражается от более плотной среды.При нормальном падении луча на поверхность клина интерференционная картина образуется на самой поверхности клина, а разность хода, между отраженными лучами от верхней и нижней граней клина, можно определить выражением
Рис.7.4
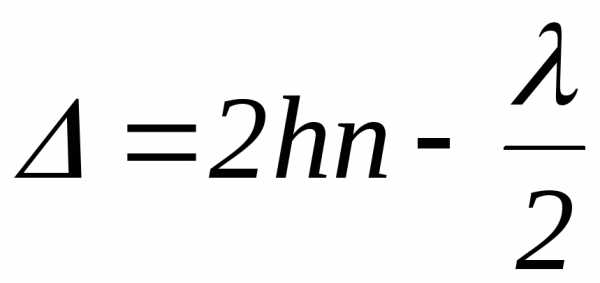 (7,2)
(7,2)Очевидно, что интерференционные полосы будут локализованы на поверхности самого клина и параллельны его ребру (рис.7.4).
Полосы равной толщины можно наблюдать и в проходящем свете.
Интерференционная картина в виде полос равной толщины широко используется на практике для контроля степени неровности различных поверхностей, плёнок, а также всевозможных покрытий. Если поверхности плёнки неровные, то полосы равной толщины принимают неправильную причудливую форму, связанную с соответствующим контуром равной толщины плёнки.
При облучении поверхности клина белым светом интерференционная картина в виде полос равной толщины оказывается окрашенной в цвета оптического спектра.
Для получения количественных соотношений, характерных для рассматриваемого явления , рассмотрим расчёт интерференционной картины в виде колец Ньютона, которая имеет место при освещении плоской монохроматической световой волной с длиной волны диэлектрической (стеклянной) линзы (рис. 7.5) с показателем преломления диэлектрика, помещённой на отражающую поверхность (зеркало).
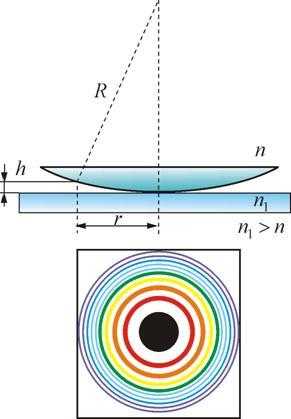
Рис.7.5
Найдём оптическую разность хода волн, отражённых от нижней поверхности линзы и от поверхности зеркала. Для облегчения расчётов заменим внутреннюю криволинейную поверхность линзы в точке отражения луча плоскостью, параллельной отражающей поверхности (рис. 7.5). В результате такого упрощения удаётся свести расчёт интерференционной картины в виде колец Ньютона к расчёту интерференционной картины в виде полос равной толщины. Полосы представляют собой концентрические эллипсы при наклонном падении света на линзу или окружности при нормальном падении. Как следует из приведенных выше рассуждений о возможности наблюдения полос равной толщины, соответствующая интерференционная картина наблюдается вблизи поверхности плёнки. В первом приближении можно полагать, что наблюдаемые интерференционные полосы располагаются непосредственно на поверхности плёнки в точке отражения волны. Тогда радиусы колец Ньютона (рис. 7.5) равны радиусам окружностей, каждая из которых соответствует точкам нижней поверхности линзы, находящихся на одинаковом расстоянии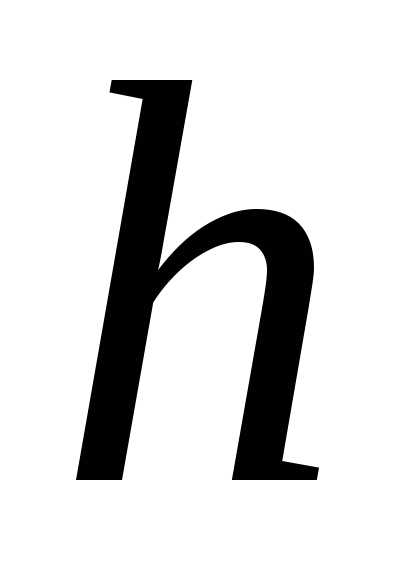 от отражающей поверхности. Если предположить, что- радиус кривизны линзы, а, то (рис. 7.5)
от отражающей поверхности. Если предположить, что- радиус кривизны линзы, а, то (рис. 7.5)(7.3)
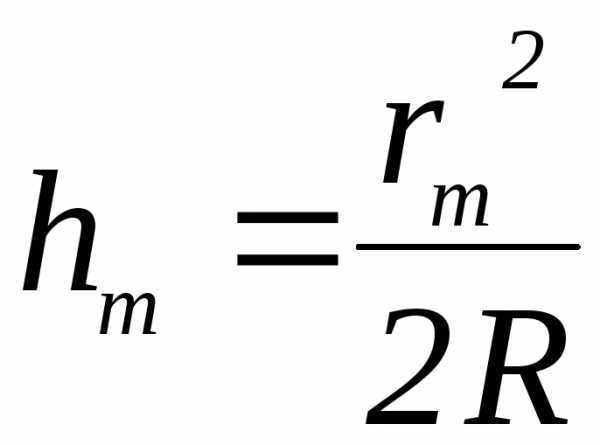 (7,4)
(7,4)
Радиусы колец Ньютона , соответствующих интерференционным максимумам с номерами, получающихся при нормальном падении световой волны к поверхности пластинки можно найти из условия формирования минимумов и максимумовприn=1
(7.5)
где длина световой волны, освещающей линзу.
Чётным значениям соответствуют светлые кольца, а нечётным - тёмные (рис. 7.5). В частности в центре картиныбудет находиться тёмное кольцо, вырождающееся в тёмную точку и соответствующее направлению противофазного сложения интерферирующих волн, так как в центреh=0 и отражение происходит от стеклянной пластинки, т.е. более плотной среды. Если линзу при наблюдении колец Ньютона поднимать вертикально вверх, то из-за увеличения проходимого лучами пути интерференционные кольца, каждое из которых соответствует некоторой постоянной разности хода, будет стягиваться к центру. При этом центр картины по мере поднятия линзы будет становиться попеременно то светлым, то тёмным.
Кольца Ньютона можно наблюдать при неправильно подобранных контактных линзах.
studfiles.net