17.Интерференция в тонких пленках. Полосы равной толщины и равного наклона. Кольца Ньютона. Применение интерференции света. Интерференция света интерференция в тонких пленках
явление и условия для его возникновения
Сегодня мы расскажем об интерференции в тонких пленках. В фокусе нашего внимания открытие, исследование и применения этого замечательного физического явления.
Определение

Прежде чем описывать какой-то закон, сначала надо понять, что за составляющие в него входят. Если этого не сделать, то читатель может пропустить важные детали, и восприятие научного факта исказится. Школьник, который пропустил одно занятие по физике из-за болезни или лени, должен обязательно разобрать эту тему самостоятельно. Потому что каждое следующее понятие опирается на предыдущее. Если упустить одно значение, непонятной будет вся остальная физика. Прежде чем приступать к выводу интерференции в тонких пленках, надо сначала дать определение явлению.
Этот феномен может относиться к любым колебательным процессам. Интерферировать могут волны ветра, моря и звука. Взаимодействие происходит даже у таких сложных квазичастиц, как коллективное колебание решетки кристаллов.
Интерференция – это явление, которое происходит при встрече в одном месте нескольких волн. Оно состоит в том, что при сложении изменяется амплитуда результирующего колебания. Это значит, что волны могут усилить, погасить друг друга или пройти дальше без изменений.
Свет

Явление интерференции в тонких пленках – это взаимодействие волн света. Так что прежде чем приступать к описанию феномена, надо пояснить природу этих колебаний.
Свет – это квант электромагнитного поля. Фотон обладает свойствами как волны, так и частицы. Пока квант движется сквозь пространство, он нерушим и вечен. Доказательством тому свет далеких галактик. Некоторые из них, возможно, уже поменяли форму или вообще перестали существовать. Но их излучение летело сквозь космос миллиарды лет, пока не достигло взгляда людей.
Основной источник света – электронные переходы в атоме. Внутри звезд происходит мощная термоядерная реакция, в результате которой выделяются все виды электромагнитного излучения. Видимый свет – только небольшой участок всей шкалы, который доступен человеческому зрению.
Свойства волны
Чтобы описать кратко интерференцию в тонких пленках, надо рассказать о волновых свойствах света. Для понимания формы идеального колебания без затухания надо только посмотреть на график синуса или косинуса в привычных декартовых координатах. Основные свойства фотона следующие:
- Длина волны. Обозначается греческой буквой λ. Длина волны – это расстояние между двумя одинаковыми фазами. Нагляднее всего эта величина демонстрируется как промежуток между двумя соседними максимумами или минимумами.
- Частота. В зависимости от вида обозначается по-разному: линейная частота – это ν, циклическая – ω, а если эта величина выражается как функция, то она пишется латинской буквой f, причем непременно курсивом. Частота и длина волны связаны соотношением λ * ν = c, где c – это скорость света в вакууме. Таким образом, зная одну величину, другую получить очень просто.
- Амплитуда. Для интерференции данное свойство волны самое важное. Это высота максимумов и минимумов колебания. Именно амплитуда изменяется, когда встречаются две волны.
- Фаза. Для единичного кванта этот фактор значения не имеет. При взаимодействии важна разница фаз. Состояние (максимум, минимум или стремление к ним), в котором пришли в одно место две волны, влияет на конечную интенсивность при интерференции.
- Поляризация. В целом это свойство описывает форму колебания. Поляризация света бывает линейной, круговой и эллиптической.
Преломление, отражение

Непосредственно явление интерференции света в тонких пленках связано еще с несколькими феноменами линейной оптики.
Встречая препятствие, свет может действовать по-разному:
- отразиться;
- преломиться;
- рассеяться;
- поглотиться.
В последнем случае фотон отдает свою энергию веществу, и там происходят какие-то изменения. Чаще всего это просто нагрев. Недаром вещь, оставленная на солнцепеке, становится очень горячей. Много разных квантов передают забытому детьми мячу свою энергию.
Рассеяние тоже подразумевает, что свет взаимодействует с материей: он поглощается и вновь излучается обратно. Часто выходящие кванты имеют другую длину волны или поляризацию.
Преломление и отражение не изменяют свойства пучка, разница лишь в направлении распространения света.
Все эти процессы участвуют, например, в формировании изображения поверхности озера.
Поведение света в тонких покрытиях

Простейшим примером пленочного покрытия является мыльная пена. Мыло увеличивает поверхностное натяжение воды. В итоге она образует очень большие площади при маленькой толщине. Мыльные пузыри переливаются всеми цветами радуги. И сейчас мы объясним, почему.
На пленку падает свет. На верхней границе покрытия часть его отражается, часть преломляется. Нас интересует второй пучок, который оказался внутри вещества. Он достигает дна, и дальше тоже часть преломляется, а часть отражается обратно внутрь пленки. Тот свет, который идет в следующую среду, для наблюдателя потерян. А вот тот, который возвращается обратно в пленку, нам как раз интересен, потому что на границе он опять преломляется и выходит в первую среду, из которой он первоначально вошел. Получается, что входящий и выходящий пучки параллельны друг другу. Это один и тот же свет, только фаза его на выходе изменилась. Разница определит, что увидит наблюдатель: светлую полосу или темную. Описанный процесс составляет сущность интерференции в тонких пленках. Кольца Ньютона, которые наблюдаются в параллельном пучке света между выпуклой линзой и плоской стеклянной пластиной, фактически имеют ту же природу. Их очень просто наблюдать: этот опыт способны произвести даже школьники на уроках физики.
Расстояние между светлыми полосами
Надеемся, читатель вполне уяснил себе механизм взаимодействия света и тонких покрытий. Теперь приведем некоторые формулы.
На выходе из пленки наблюдается картина светлых и темных областей. Площади, на которых конечная картина имеет одну и ту же освещенность, называется полосами равного наклона. Интерференция в тонких пленках дает нам следующую формулу для их расчета:
2m * λ = (2nh * cosβ ± λ) / 2.
Здесь: λ – длина волны падающего излучения, m – порядок интерференции, β – угол между преломленным в первый раз пучком и нормалью к поверхности, n – показатель преломления пленки, а h – ее толщина.
Следует отметить, что данное условие покажет геометрическое место точек наиболее светлых областей интерференционной картины.
Таким образом расположены только те пучки, которые падают на поверхность пленки под одним и тем же углом. Именно поэтому они называются полосами равного наклона.
Фотоаппараты и очки

Школьник, который находит физику скучным предметом, наверняка задает себе вопрос: «Зачем все это нужно?». Тем не менее взаимодействие света и тонких покрытий используется в повседневной жизни достаточно широко.
На линзах любой фото- и телеаппаратуры есть напыление: тончайшая прозрачная пленка. Ее толщина подобрана так, чтобы камера не давала зеленых бликов (свет этой длины волны гасит сам себя, проходя через слой на поверхности стекла). Такое решение делает изображение контрастным и ярким. Ведь человек лучше всего видит зеленый спектр и недостатки этого цвета воспринимает наиболее четко.
Просветляющее напыление наносится также на линзы микроскопов и телескопов. И не обязательно толщина пленки соответствует зеленому цвету. Если ученый исследует процессы с инфракрасным или ультрафиолетовым излучением, аппаратура помогает ему именно в этом диапазоне.
Лазеры

Также интерференция применяется в лазерах, но этот факт известен немногим.
Сегодня без лазеров не обходится ни один из видов человеческой деятельности. Устройство состоит из трех частей – накачки, рабочего тела и отражателя. Зеркало расположено на торцах основного излучающего материала. Его предназначение – собирать генерируемые фотоны конкретной длины волны в одном направлении. Этот элемент прибора часто представляет собой ряд тонких пленок, интерференция на которых позволяет проходить дальше только нужному излучению.
fb.ru
4. Интерференция света в тонких пленках
Многим людям приходилось наблюдать радужную окраску мыльных пленок; цвета побежалости закаленных стальных деталей, покрытых тонким прозрачным слоем окисных пленок; тонких пленок нефти, бензина, масел, плавающих на поверхности воды.
Рис. 5
Все эти явления вызваны интерференцией света в тонких пленках. Интерференцию света в тонких пленках можно наблюдать в проходящем или отраженном свете. Рассмотрим интерференцию света на отражение от тонкой прозрачной пленки (пластинки) толщиной d с абсолютным показателем преломления n (рис. 5). Пластинка (пленка) находится в вакууме (n1 = nвак = 1, - длина волны света в вакууме, причем n > n1).Пусть на пленку падает плоская монохроматическая волна под углом (луч АО). В т. О на верхней поверхности этот луч частично отражается (луч ОМ) и частично преломляется (луч ОС). Преломленный луч ОС, достигнув нижней поверхности пленки, в т. С испытывает, в свою очередь отражение (луч СЕ) и преломление (луч СN), переходя снова в вакуум.
Отраженный луч СЕ на верхней поверхности пленки в т. Е испытывает частичное отражение (луч ЕК) и частичное преломление (луч ЕР).
Преломленный луч ЕР и отраженный луч ОМ когерентны и при наложении интерферируют. Действительно, если на их пути поставить собирательную линзу, то в т. К на экране можно наблюдать интерференционную картину на отражение, максимум и минимум которой будут определяться оптической разностью хода, возникающей между лучами ОМ и ЕР от точки 0 до плоскости ЕМ, т. е.
(12)
где слагаемое /2 возникает из-за потери полуволны при отражении света на границе раздела вакуум-пленка в т. О.
Согласно рис. 5 ОС = СЕ = 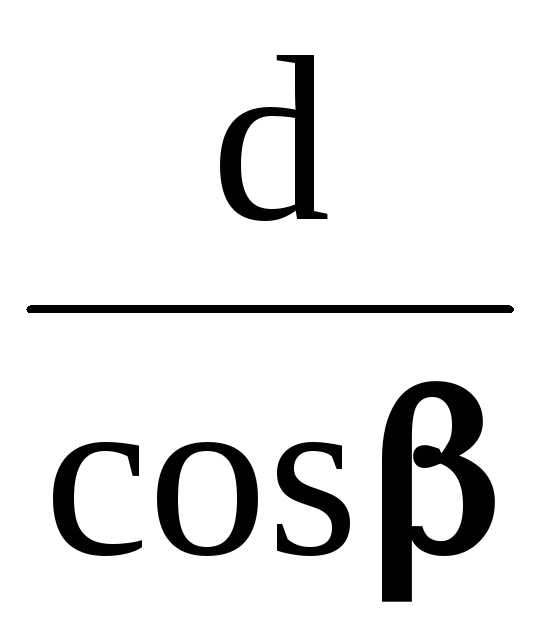 , ОМ = ОЕsin = 2dntgsin.
, ОМ = ОЕsin = 2dntgsin.
Применяя закон преломления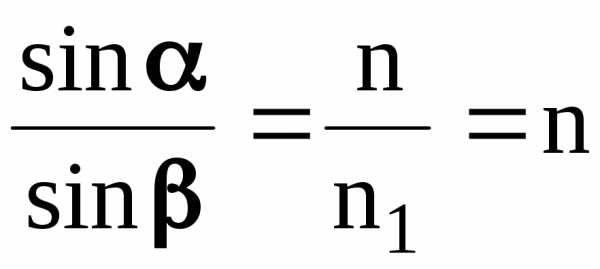 , (n1 = 1)
, (n1 = 1)
получаем после подстановки в (5) оптическую разность хода лучей на отражение
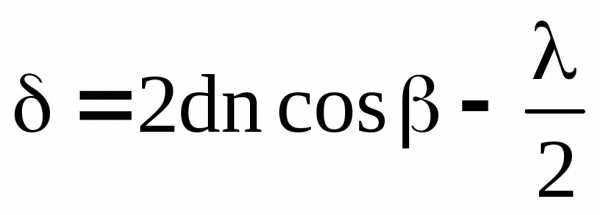 (13)
(13)
или . (14)
При мах = 2m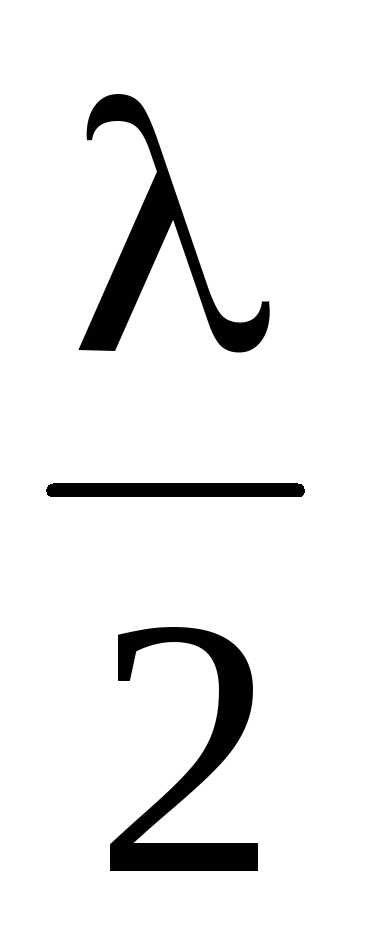 максимум интерференции в тонких пленках на отражение удовлетворяет условию . (15)
максимум интерференции в тонких пленках на отражение удовлетворяет условию . (15)
При min = (2m + 1)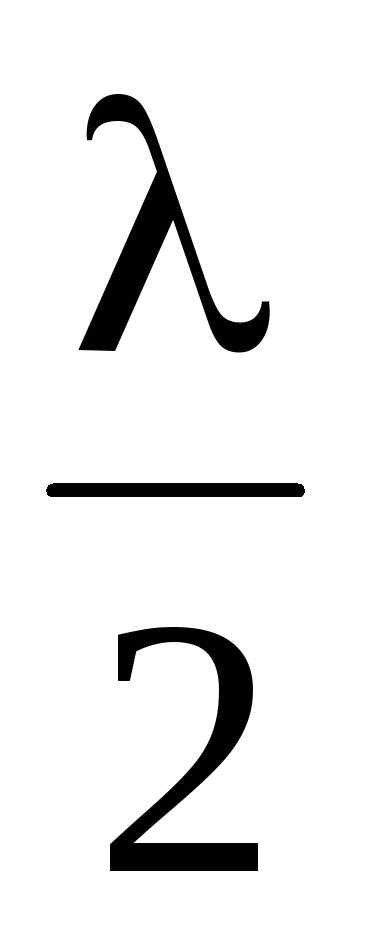 получаем условие минимума интерференции в тонких пленках на отражение, т. е.
получаем условие минимума интерференции в тонких пленках на отражение, т. е.
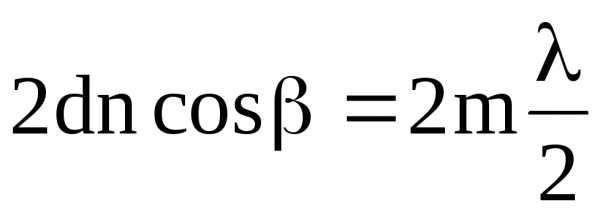 . (16)
. (16)
Аналогичный расчет можно провести для интерференции в тонких пленках на просвет в т. Q. Однако дополнительной оптической разности хода в этом случае не наблюдается. Поэтому максимум интерференции в тонких пленках на просвет соответствует условию минимума на отражение - формула (16) и, наоборот, минимум интерференции в тонких пленках на просвет соответствует максимуму на отражение - формула (15).
При освещении пленки белым светом для некоторых длин волн будет выполняться условие максимума, а для других - условие минимума, поэтому пленка в отраженном свете выглядит окрашенной.
5. Полосы равного наклона
При падении сходящегося (расходящегося) пучка света на плоскопараллельную пластинку (пленку) при интерференции могут возникнуть полосы равного наклона. Для каждой пары лучей 1 и 1*, 2 и 2* (рис. 6) оптическая разность хода определяется формулой
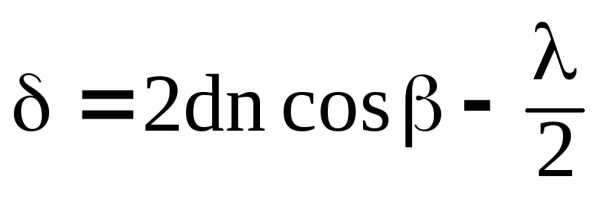 .
.
Для каждой из пар значений - различны, так как 1 2.
При наблюдении интерференционной картины используют собирательную линзу (Л) и экран (Э). В каждой точке экрана собираются и интерферируют лучи, которые после отражения от пленки параллельны прямым линиям, соединяющими их с оптическим центром линзы 0 (рис. 6). Например, лучи 1 и 1* - в т. В, лучи 2 и 2* - в т. А и т. д.
Рис. 6
Любая линза не создает дополнительной оптической разности хода между лучами, фокусируемыми ею на экране.Интерференционная картина на экране имеет вид чередующихся светлых и темных полос (полосы равного наклона), каждой из которых соответствует определенное значение угла падения .
Максимум или минимум интерференции на отражение в этом случае зависти от угла падения лучей. При освещении пленки белым светом на экране возникает система разноцветных полос равного наклона. Если оптическая ось линзы перпендикулярна поверхности пленки, то полосы равного наклона имеют вид чередующихся концентрических темных и светлых колец. В отсутствии линзы лучи 1 и 1*, 2 и 2* уходят в бесконечность.
Следовательно, полосы равного наклона локализованы в бесконечности. Это явление используется на практике для точного контроля степени параллельности тонких пленок (пластин). Изменение толщины пленки на 108 м можно обнаружить по искажению формы колец равного наклона.
studfiles.net
| Интерференционные полосы равного наклона. При освещении тонкой пленки происходит наложение волн от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала. Рассмотрим сначала плоскопараллельную пластинку толщины с показателем преломления (рис. 2.11). Пусть на пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света, один из которых образовался за счет отражения от верхней поверхности пластинки, второй – вследствие отражения от нижней поверхности. Каждый из этих пучков представлен на рис. 2.11 только одним лучом. При входе в пластинку и при выходе из нее пучок 2 претерпевает преломление. Кроме двух пучков и , пластинка отбрасывает вверх пучки, возникающие в результате трех-, пяти- и т.д. кратного отражения от поверхностей пластинки. Однако ввиду малой интенсивности их можно не принимать во внимание. Рассмотрим интерференцию лучей, отраженных от пластинки. Поскольку на пластинку падает плоская волна, то фронт этой волны представляет собой плоскость, перпендикулярную лучам 1 и 2. На рис. 2.11 прямая ВС представляет собой сечение волнового фронта плоскостью рисунка. Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, будет
где – длина отрезка ВС, а – суммарная длина отрезков АО и ОС. Показатель преломления среды, окружающей пластинку, полагаем равным единице. Из рис. 2.11 видно, что , . Подстановка этих выражений в (2.13) дает . Воспользуемся законом преломления света: ; и учтем, что , тогда для разности хода получим следующее выражение: . При вычислении разности фаз между колебаниями в лучах и нужно, кроме оптической разности хода D, учесть возможность изменения фазы при отражении в точке С. В точке С отражение волны происходит от границы раздела среды оптически менее плотной со средой оптически более плотной. Поэтому фаза волны претерпевает изменение на p. В точке отражение происходит от границы раздела среды оптически более плотной со средой оптически менее плотной, и скачка фазы в этом случае не происходит. Качественно это можно представить себе следующим образом. Если толщину пластинки устремить к нулю, то полученная нами формула для оптической разности хода дает . Поэтому при наложении лучей и должно происходить усиление колебаний. Но это невозможно, так как бесконечно тонкая пластинка вообще не может оказывать влияния на распространение света. Поэтому волны, отраженные от передней и задней поверхности пластинки, должны при интерференции гасить друг друга. Их фазы должны быть противоположны, то есть оптическая разность хода D при d→0 должна стремиться к . Поэтому к прежнему выражению для D нужно прибавить или вычесть , где λ0 – длина волны в вакууме. В результате получается:
Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (2.14). Эти волны могут интерферировать, если оптическая разность хода не превышает длину когерентности. Последнее требование для солнечного излучения приводит к тому, что интерференция при освещении пластинки наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра. Практически интерференцию от плоскопараллельной пластинки наблюдают, поставив на пути отраженных пучков линзу, которая собирает пучки в одной из точек экрана, расположенного в фокальной плоскости линзы. Освещенность в этой точке зависит от оптической разности хода. При получаются максимумы, при – минимумы интенсивности. Следовательно, условие максимумов интенсивности имеет вид:
а минимумов:
Эти соотношения получены для отраженного света.
В результате на экране возникнет совокупность чередующихся темных и светлых круговых полос с общим центром в точке О. Каждая полоса образована лучами, падающими на пластину под одинаковым углом. Поэтому получающиеся в этом случае интерференционные полосы называютсяполосами равного наклона. Согласно (2.15) положение максимумов интенсивности зависит от длины волны , поэтому в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных цветов, и интерференционная картина приобретет радужную окраску. Для наблюдения полос равного наклона экран должен располагаться в фокальной плоскости линзы, так, как его располагают для получения бесконечно удаленных предметов. Поэтому говорят, что полосы равного наклона локализованы в бесконечности. Роль линзы может играть хрусталик глаза, а экрана – сетчатка глаза. Интерференционные полосы равной толщины.Возьмем теперь пластинку в виде клина. Пусть на нее падает параллельный пучок лучей (рис. 2.13). Но теперь лучи, отразившись от разных поверхностей пластинки, не будут параллельными. Если расположить экран Э так, чтобы он проходил через точки и , на экране возникнет интерференционная картина. При малом угле клина разность хода лучей, отраженных от его верхней и нижней поверхностей, можно с достаточной степенью точности вычислить по формуле , полученной для плоскопараллельной пластинки, беря в качестве толщину клина в месте падения на нее лучей. Поскольку разность хода лучей, отразившихся от разных участков клина, теперь неодинакова, освещенность будет неравномерной – на экране появятся светлые и темные полосы. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины. Таким образом, интерференционная картина, получающаяся при отражении от клина плоской волны, оказывается локализованной в некоторой области вблизи поверхности клина. По мере удаления от вершины клина растет оптическая разность хода, и интерференционная картина становится все менее отчетливой.
При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки будет иметь радужную окраску. В реальных условиях при наблюдении, например, радужных цветов на мыльной пленке изменяется как угол падения лучей, так и толщина пленки. В этом случае наблюдаются полосы смешанного типа. Полосы равной толщины легко наблюдать на плоской проволочной рамке, которую окунули в мыльный раствор. Затягивающая её мыльная плёнка покрывается горизонтальными интерференционными полосами, получившимися при интерференции волн, отразившихся от разных поверхностей пленки (рис. 2.14). С течением времени мыльный раствор стекает, и интерференционные полосы съезжают вниз. Если проследить за поведением сферического мыльного пузыря, то легко обнаружить, что его поверхность покрыта цветными кольцами, медленно сползающими к его основанию. Смещение колец говорит о постепенном утончении стенок пузыря. Кольца Ньютона
Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. В этом случае и . Из рис. 2.15 видно, что , где – радиус кривизны линзы, – радиус окружности, всем точкам которой соответствует одинаковый зазор . Величиной можно пренебречь, тогда . Чтобы учесть возникающее при отражении от пластинки изменение фазы на p, нужно добавить к разности хода :
В точках, для которых , возникнут максимумы интенсивности, а в точках, для которых – минимумы интенсивности. Оба условия можно объединить в одно:
четным будут соответствовать максимумы, а нечетным – минимумы интенсивности. Подставив (2.18) в (2.17), получим радиусы темных и светлых колец Ньютона:
Четным соответствуют радиусы светлых колец, нечетным – радиусы темных колец. Значению соответствует , то есть в месте касания пластинки и линзы наблюдается минимум интенсивности, обусловленный изменением фазы на p при отражении световой волны от пластинки.
На рис. 2.16 представлен вид интерференционных колец Ньютона в красном и зеленом свете. Так как длина волны красного света больше, чем зеленого, то радиусы колец в красном свете больше радиусов колец с таким же номером в зеленом свете. Если в установке Ньютона линзу перемещать вверх параллельно самой себе, то из-за увеличения толщины воздушной прослойки каждая окружность, соответствующая постоянной разности хода, будет стягиваться к центру картины. Достигнув центра, интерференционное кольцо превращается в кружок, исчезающий при дальнейшем перемещении линзы. Таким образом, центр картины будет попеременно становиться то светлым, то темным. Одновременно на периферии поля зрения будут зарождаться и перемещаться к центру новые интерференционные кольца, пока каждое из них не исчезнет в центре картины. При перемещении линзы непрерывно вверх пропадают кольца самых низких порядков интерференции и зарождаются кольца более высоких порядков. Пример Просветление оптики Просветление оптики делается для уменьшения коэффициентов отражения поверхностей оптических деталей путём нанесения на них одной или нескольких непоглощающих плёнок. Без просветляющих плёнок потери на отражение света могут быть очень большими. В системах с большим числом поверхностей, например, в сложных объективах, потери света могут достигать 70 % и более, что ухудшает качество изображений, формируемых такими оптическими системами. Устранить это можно с помощью просветления оптики, которое является одним из важнейших применений интерференции в тонких пленках. При отражении света от передней и задней поверхности пленки, нанесенной на оптическую деталь, в отраженном свете образуется минимум интенсивности в результате интерференции, а следовательно, в проходящем свете будет максимум интенсивности для этой длины волны. При нормальном падении света эффект будет максимален, если толщина тонкой плёнки равна нечётному числу четвертей длины световой волны в материале плёнки. Действительно, в этом случае потери половины длины волны при отражении не происходит, так как и на верхней, и на нижней поверхностях пленки волна отражается от границы раздела среды оптически менее плотной и оптически более плотной. Поэтому условие максимума интенсивности примет вид . Отсюда получим . Изменяя толщину просветляющей плёнки, можно сместить минимум отражения в различные участки спектра. |
stydopedia.ru
Интерференция света в тонких пленках
7
Л3-3Интерференция света в тонких пленках
Пластинка постоянной толщины.При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при определенных условиях могут интерферировать.
Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна (параллельный пучок света). В результате отражений от поверхностей пластинки, часть света возвращается в исходную среду. Отраженный свет состоит из лучей, испытавших одно-, трех-, пяти- и т.д. кратное отражение. Ввиду малой интенсивности лучи трехкратного отражения и выше принимать в расчет не будем (при n1.5 от поверхности пластинки отражается примерно 4%падающего светового потока). Однократно отраженные от пластинки лучи1и2когерентны, если оптическая разность их хода меньше длины когерентности падающей волны. Если на пути лучей поставить собирающую линзу, то на экране, совмещенном с фокальной плоскостью линзы, возникнет интерференционная картина. Роль линзы может играть хрусталик, а экрана – сетчатка глаза. В этом случае глаз должен быть аккомодирован (наведен на резкость) на бесконечность.
Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки Oдо точкиP
. Согласно рис.,. Учитывая закон преломления, получим
.
При вычислении разности колебаний в лучах 1и2нужно, кроме оптической разности хода, учесть возможность изменения фазы волны при отражении. В точкеOотражение происходит от оптически более плотной среды. Поэтому фаза отраженной волны изменяется на(для определенности считаем, что происходит потеря полуволны). В точкеCотражение происходит от оптически менее плотной среды, так что скачка фазы не происходит. С учетом потери полуволны для оптической разности хода получим
. (1)
В точке Pбудет интерференционный максимум, если
, (2а) и минимум, если
. (2б) Выясним условия, при которых эти волны окажутся когерентными и смогут интерферировать. Для того, чтобы имела место временная когерентность, разность хода (1) не должна превышать длину когерентности. Следовательно, должно выполнятся условие
. В данном соотношении, поэтому условию временной когерентности можно придать вид
. (3) Положив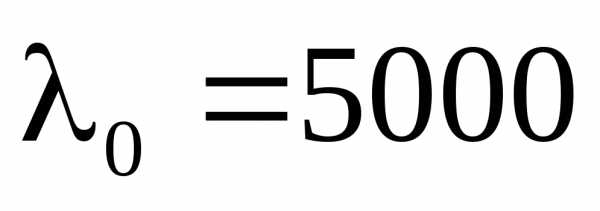 Å и
Å и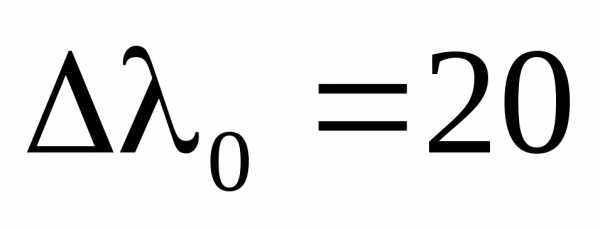 Å, получим предельное значение толщины пластинки – 0,06 мм. Пусть пластинка освещается рассеянным монохроматическим светом (рис.). В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные некоторому направлению, после отражения соберутся в одной точке и создадут в ней освещенность, определяемую значением оптической разности хода. Лучи, идущие в другом направлении, соберутся в другой точке и т.д. В результате возникает система чередующихся светлых и темных полос (если линза параллельна пластинке, полосы имеет вид концентрических колец с центром в фокусе линзы). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом. Поэтому получающиеся интерференционные полосы носят названиеполос равного наклона.
Å, получим предельное значение толщины пластинки – 0,06 мм. Пусть пластинка освещается рассеянным монохроматическим светом (рис.). В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные некоторому направлению, после отражения соберутся в одной точке и создадут в ней освещенность, определяемую значением оптической разности хода. Лучи, идущие в другом направлении, соберутся в другой точке и т.д. В результате возникает система чередующихся светлых и темных полос (если линза параллельна пластинке, полосы имеет вид концентрических колец с центром в фокусе линзы). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом. Поэтому получающиеся интерференционные полосы носят названиеполос равного наклона.
Согласно формуле (2а) положение максимумов зависит от длины волны 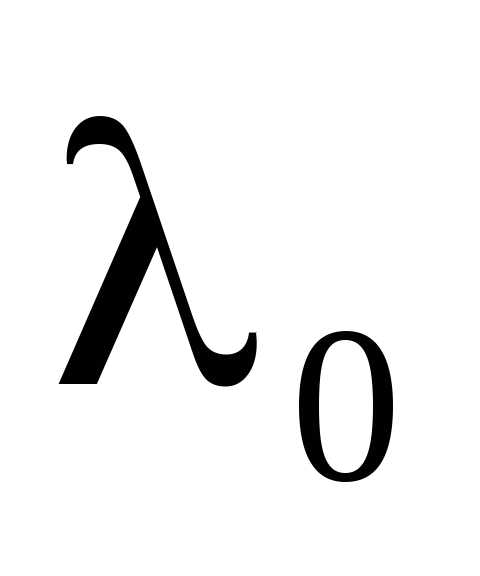 . Поэтому в белом свете интерференционная картина приобретает радужную окраску. Возможность наблюдения интерференционной картины в белом свете определяется способностью глаза различать оттенки цвета. Средний глаз отличает цвета, отличающиеся по длине волны не менее чем на 20 Å. Именно такое значение
. Поэтому в белом свете интерференционная картина приобретает радужную окраску. Возможность наблюдения интерференционной картины в белом свете определяется способностью глаза различать оттенки цвета. Средний глаз отличает цвета, отличающиеся по длине волны не менее чем на 20 Å. Именно такое значение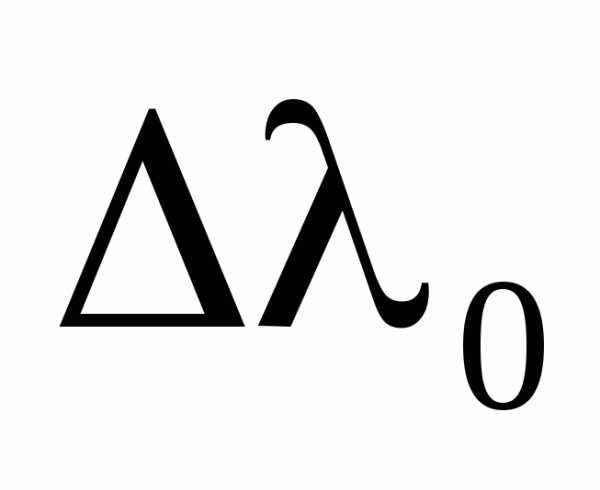 взято при оценке толщины пластинки.
взято при оценке толщины пластинки.
Пластинка переменной толщины.Пусть на клин с острым углом (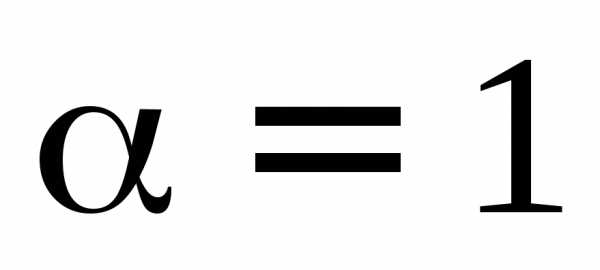 ) падает плоская световая волна. При отражении падающего луча1от верхней и нижней поверхностей клина возникают лучи1 и1соответственно. При распространении они пересекаются в точке
) падает плоская световая волна. При отражении падающего луча1от верхней и нижней поверхностей клина возникают лучи1 и1соответственно. При распространении они пересекаются в точке . Можно показать, что аналогичные точки пересечения других пар отраженных лучей лежат в одной плоскости, проходящей через вершину клинаO. Временная когерентность будет выполняться для тех лучей, для которых толщина клина в месте отражения удовлетворяет условию (3). Допустим, что это условие выполняется для всего клина или хотя бы для его части. Тогда в плоскости экрана
. Можно показать, что аналогичные точки пересечения других пар отраженных лучей лежат в одной плоскости, проходящей через вершину клинаO. Временная когерентность будет выполняться для тех лучей, для которых толщина клина в месте отражения удовлетворяет условию (3). Допустим, что это условие выполняется для всего клина или хотя бы для его части. Тогда в плоскости экрана будет наблюдаться интерференционная картина в виде полос, параллельных ребру клинаO. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называютполосами равной толщины.
будет наблюдаться интерференционная картина в виде полос, параллельных ребру клинаO. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называютполосами равной толщины.
При другом расположении экрана (например,  и
и ) интерференция также возможна. Поскольку, в этом случае на экране пересекаются отражения разных лучей, то соответствующие падающие лучи должны быть пространственно когерентны (например, когерентны лучи1и2– экран
) интерференция также возможна. Поскольку, в этом случае на экране пересекаются отражения разных лучей, то соответствующие падающие лучи должны быть пространственно когерентны (например, когерентны лучи1и2– экран или1и3– экран
или1и3– экран ). При ограниченной пространственной когерентности область локализации интерференционной картины (т.е. область пространства, располагая в которой экран можно наблюдать на нем интерференционную картину) также оказывается ограниченной. Причем эта область тем уже, чем меньше степень пространственной когерентности падающей волны.
). При ограниченной пространственной когерентности область локализации интерференционной картины (т.е. область пространства, располагая в которой экран можно наблюдать на нем интерференционную картину) также оказывается ограниченной. Причем эта область тем уже, чем меньше степень пространственной когерентности падающей волны.
Рассмотрим условия соблюдения пространственной когерентности. При рассмотрении считаем толщину пластинки неизменной. Из рис. видно, что расстояние между падающими лучами 1и2равно
. Если принять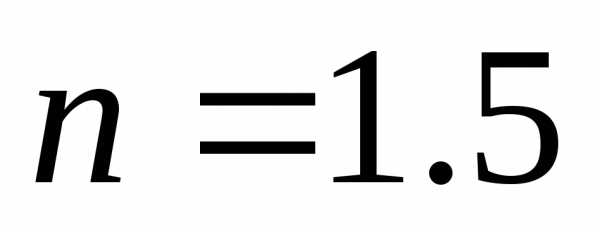 , то для
, то для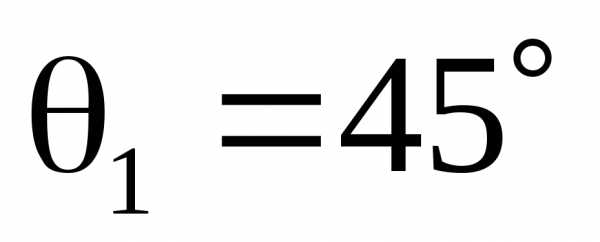 получается(для нормального падения
получается(для нормального падения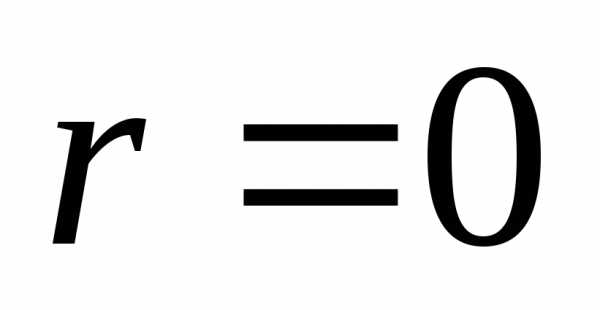 ). Радиус когерентности солнечного света имеет значение порядка 0,05 мм. Следовательно, для возникновения интерференции в этих условиях должно выполнятьсяd 0.05 мм. Таким образом, требования временной и пространственной когерентности дают близкие значения толщины пластинки, при которой в солнечном свете будет наблюдаться интерференция. При освещении светом с большей степенью когерентности интерференция наблюдается и при отражении от более толстых пластинок или пленок.
). Радиус когерентности солнечного света имеет значение порядка 0,05 мм. Следовательно, для возникновения интерференции в этих условиях должно выполнятьсяd 0.05 мм. Таким образом, требования временной и пространственной когерентности дают близкие значения толщины пластинки, при которой в солнечном свете будет наблюдаться интерференция. При освещении светом с большей степенью когерентности интерференция наблюдается и при отражении от более толстых пластинок или пленок.
Практически полосы равной толщины наблюдают визуально либо поместив линзу и за ней экран. При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки или пленки будет представляться окрашенной. Такую окраску имеют, например, расплывшиеся на поверхности воды тонкие пленки нефти или масла, а также мыльные пленки. Цвета побежалости, возникающие на поверхности стальных изделий при их закалке, также обусловлены интерференцией от пленки прозрачных окислов.
Сопоставим два рассмотренных случая интерференции при отражении от тонких пленок. Полосы равного наклона получаются при освещении пластинки постоянной толщины () рассеянным светом, в котором содержатся лучи разных направлений. Локализованы полосы равного наклона в бесконечности. Полосы равной толщины наблюдаются при освещении пластинки непостоянной толщины параллельным пучком света (). Локализованы полосы раной толщины вблизи пластинки. В реальных условиях изменяется как угол падения лучей, так и толщина пленки. В этом случае наблюдается полосы смешанного типа.
Кольца Ньютона.Классическим примером полос равной толщины являютсякольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис). Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинками и линзой (вследствие большой толщины пластинки и линзы, отраженные от других поверхностей лучи в образовании интерференционной картины не участвуют). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении – эллипсов. Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. Из рис. следует, что
, гдеR– радиус кривизны линзы,r– радиус окружности, которой соответствует зазор толщиныd. Таким образом,
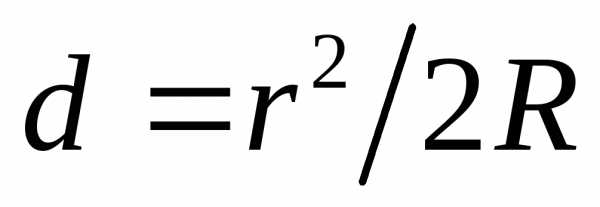 . С учетом потери полуволны, возникающей при отражении от пластинки, оптическая разность хода лучей1и1равна
. С учетом потери полуволны, возникающей при отражении от пластинки, оптическая разность хода лучей1и1равна
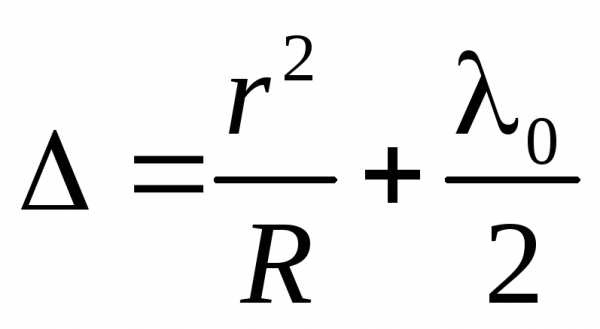 .
.
Используя условия максимума (2а) и минимума (2б), получим выражения для радиусов m-го светлого иm-го темного кольца соответственно
, (4а). (4б)
Многолучевая интерференция.До сих пор рассматривалась двухлучевая интерференция. Теперь исследуем случай, когда интерферируют много световых лучей.
Допустим, что в данную точку экрана приходит Nлучей одинаковой интенсивности, причем фаза каждого следующего луча сдвинута относительного фазы предыдущего на одну и ту же величину. Представим световые колебания в комплексной форме с помощью рекуррентного соотношения
. Результирующее колебание определяется суммой геометрической прогрессии
. Расчет интенсивности, возникающей при интерференции, дает значение
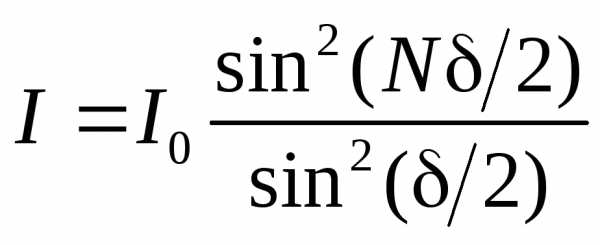 , (5) где
, (5) где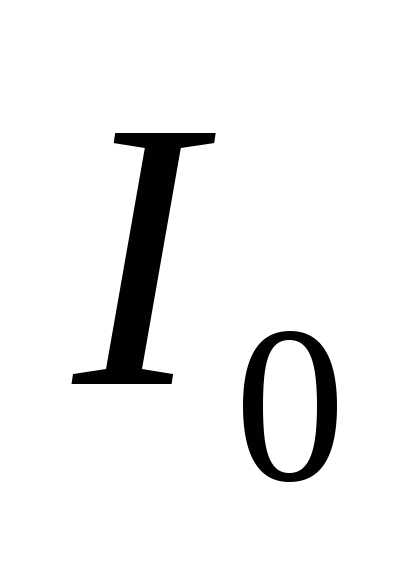 – интенсивность, создаваемая каждым лучом в отдельности.
– интенсивность, создаваемая каждым лучом в отдельности.
При значениях () результирующая интенсивность оказывается равной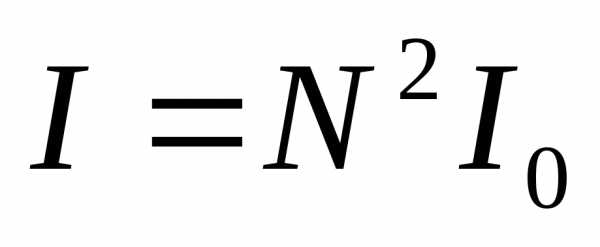 , что соответствуетглавным максимумам. Числоmназываетсяпорядкомглавного максимума. В промежутке между главными максимумами располагается
, что соответствуетглавным максимумам. Числоmназываетсяпорядкомглавного максимума. В промежутке между главными максимумами располагается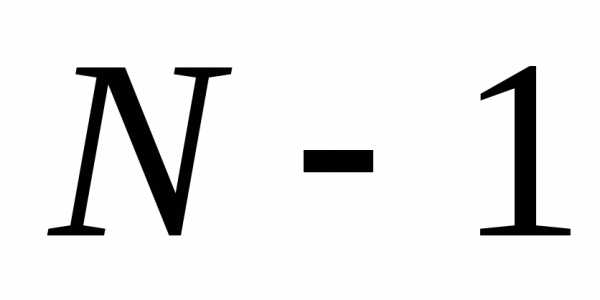 минимум интенсивности. В свою очередь между
минимум интенсивности. В свою очередь между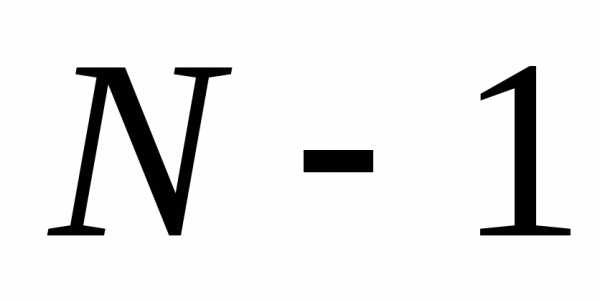 минимумами располагается
минимумами располагается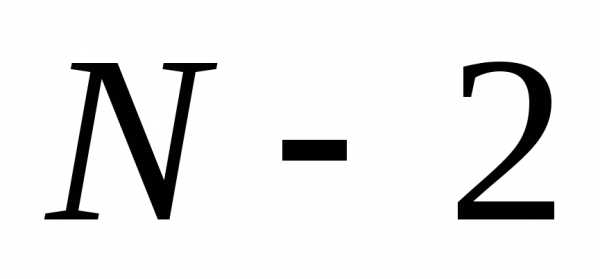 вторичных максимумов. Наибольшей интенсивностью обладают вторичные максимумы, ближайшие к главным максимумам. При большомNони имеют интенсивность в22 раза меньшую, чем интенсивность главного максимума. Ситуация близкая к многолучевой интерференции возникает в дифракционной решетке, которая будет рассмотрена позднее.
вторичных максимумов. Наибольшей интенсивностью обладают вторичные максимумы, ближайшие к главным максимумам. При большомNони имеют интенсивность в22 раза меньшую, чем интенсивность главного максимума. Ситуация близкая к многолучевой интерференции возникает в дифракционной решетке, которая будет рассмотрена позднее.
Теперь рассмотрим интерференцию очень большого числа лучей (), интенсивность которых убывает в геометрической прогрессии. Предположим, что колебания имеют вид
, где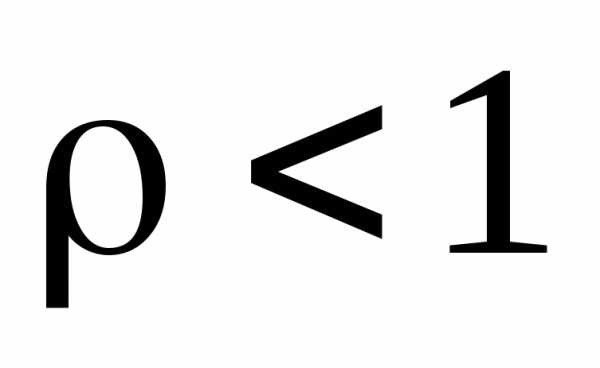 – постоянная величина. Результирующее колебание описывается суммой геометрической прогрессии
– постоянная величина. Результирующее колебание описывается суммой геометрической прогрессии
с интенсивностью равной
, (6) где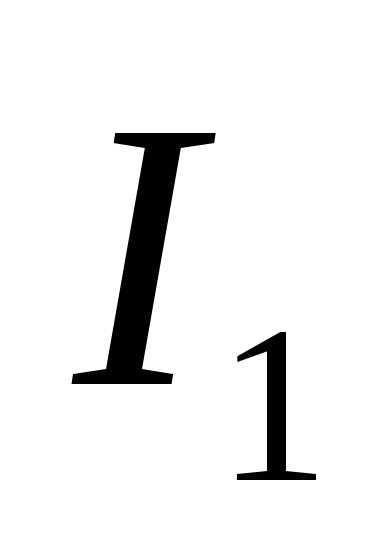 – интенсивность первого (наиболее интенсивного) луча.
– интенсивность первого (наиболее интенсивного) луча.
При значениях () выражение (6) имеет максимумы
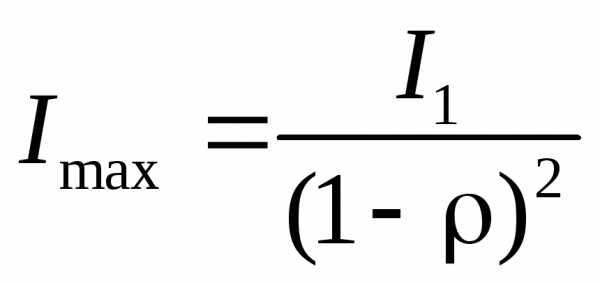 . В промежутках между максимумами функция изменяется монотонно, достигая в середине промежутка минимальное значение
. В промежутках между максимумами функция изменяется монотонно, достигая в середине промежутка минимальное значение
. Таким образом,
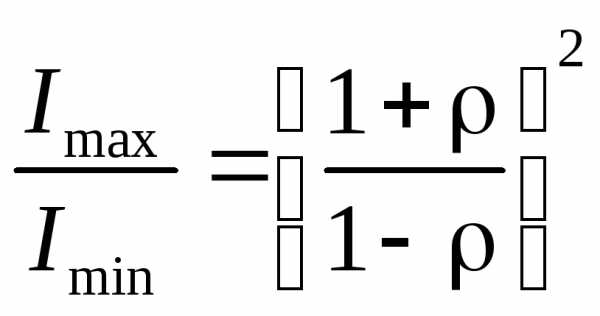 . Интерференционная картина имеет вид узких резких линий на практически темном фоне. Практически случай большого числа лучей с убывающей интенсивностью осуществляется в интерферометреФабри-Перо.
. Интерференционная картина имеет вид узких резких линий на практически темном фоне. Практически случай большого числа лучей с убывающей интенсивностью осуществляется в интерферометреФабри-Перо.
Применение интерференции света.
Просветление оптики. Явление интерференции применяется для улучшения качества оптических приборов и получения высокоотражающих покрытий. Прохождение света через каждую преломляющую поверхность линзы сопровождается отражением4%падающего потока (при показателе преломления стекла1,5). Так как современные объективы состоят из большого количества линз, то число отражений в них велико, а поэтому велики и потери светового потока. Для устранения этого и других недостатков осуществляют так называемоепросветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления, меньшим, чем у материала линзы. При отражении света от границ раздела воздух–пленка и пленка–стекло возникает интерференция отраженных лучей. Толщину пленкиdи показатели преломления стекла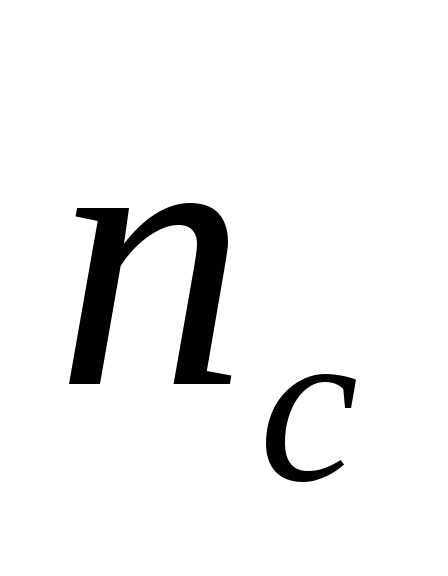 и пленкиnподбираются так, чтобы отраженные волны гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна. Расчет показывает, что амплитуды отраженных лучей равны, если
и пленкиnподбираются так, чтобы отраженные волны гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна. Расчет показывает, что амплитуды отраженных лучей равны, если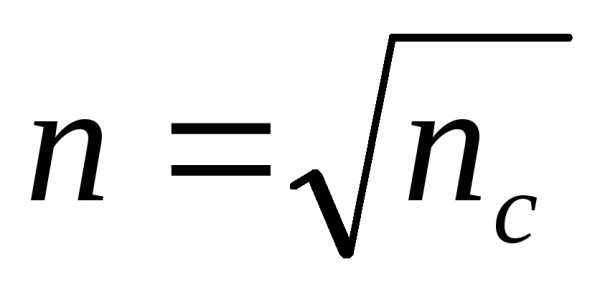 . Так как
. Так как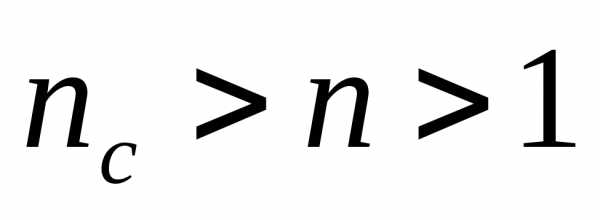 , то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (свет падает нормально)
, то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (свет падает нормально)
. Обычно принимают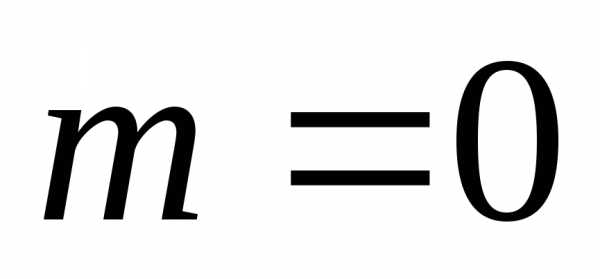 , тогда
, тогда
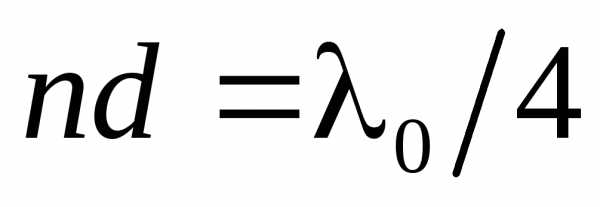 . Так как добиться одновременного гашения для всех длин волн невозможно (показатель преломления зависит от длины волны), то это делается для цвета с(к нему наиболее чувствителен глаз). Поэтому объективы с просветленной оптикой имеют синевато-красный оттенок.
. Так как добиться одновременного гашения для всех длин волн невозможно (показатель преломления зависит от длины волны), то это делается для цвета с(к нему наиболее чувствителен глаз). Поэтому объективы с просветленной оптикой имеют синевато-красный оттенок.
Интерференционные светофильтры.Многолучевую интерференцию можно осуществить в многослойной системе чередующихся пленок с разными показателями преломления (но одинаковой оптической толщиной, равной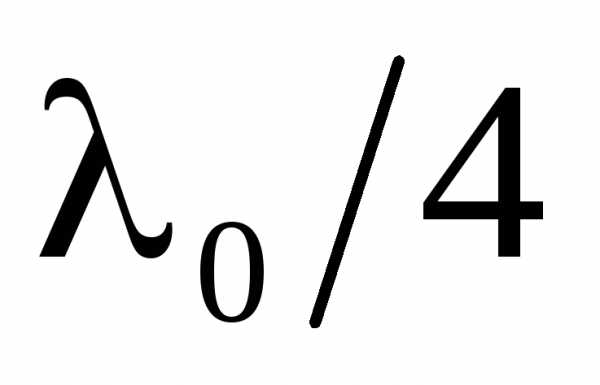 ). При прохождении света возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленок
). При прохождении света возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленок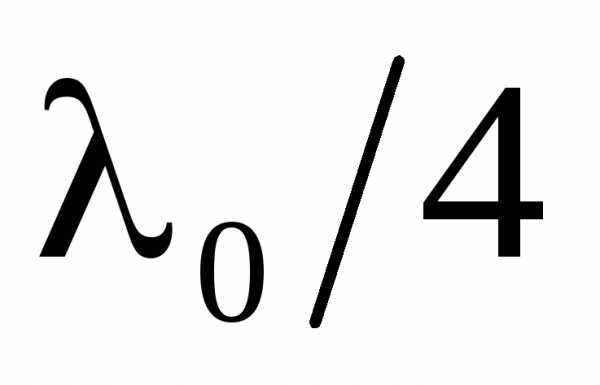 будут взаимно усиливаться, т.е. коэффициент отражения возрастает. Подобные отражатели применяются в лазерной технике, а также используются для создания интерференционных светофильтров.
будут взаимно усиливаться, т.е. коэффициент отражения возрастает. Подобные отражатели применяются в лазерной технике, а также используются для создания интерференционных светофильтров.
Интерферометры.Явление интерференции применяется в очень точных измерительных приборах –интерферометрах. На рис. изображена схемаинтерферометра Майкельсона. Пучок света от источникаSпадает на пластинку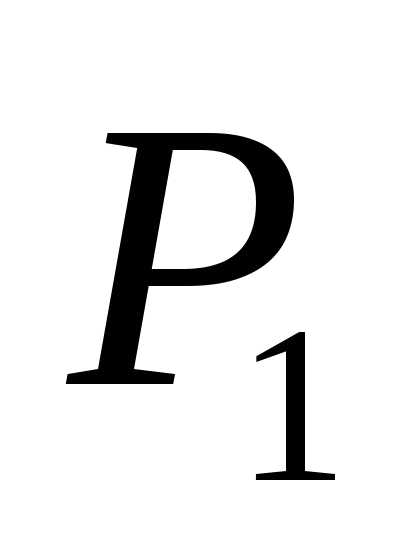 , покрытую тонким слоем серебра (благодаря чему коэффициент отражения близок к 0,5). Дальнейший ход интерферирующих лучей ясен из рисунка. На пути луча1ставится точно такая, как
, покрытую тонким слоем серебра (благодаря чему коэффициент отражения близок к 0,5). Дальнейший ход интерферирующих лучей ясен из рисунка. На пути луча1ставится точно такая, как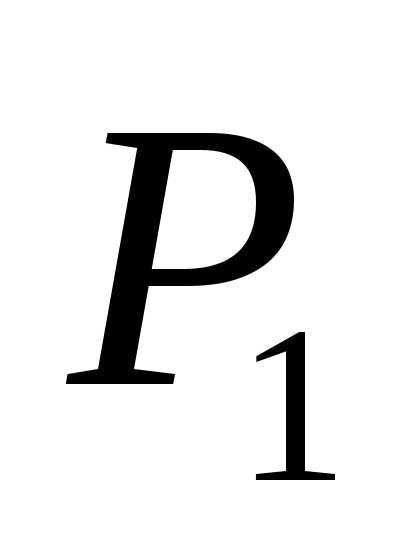 , но не посеребренная пластинка
, но не посеребренная пластинка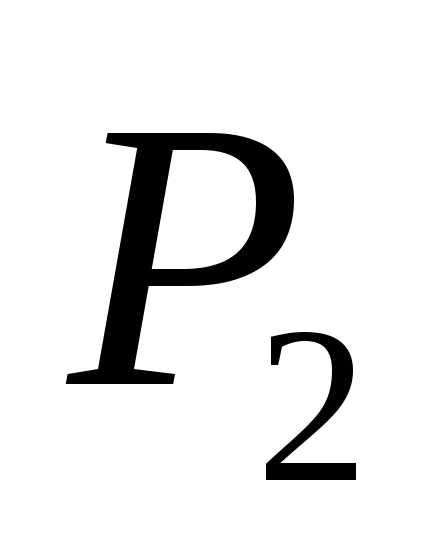 . Она уравнивает пути лучей1и2в стекле. Интерференционная картина наблюдается с помощью зрительной трубы.
. Она уравнивает пути лучей1и2в стекле. Интерференционная картина наблюдается с помощью зрительной трубы.
Интерференционная картина соответствует интерференции в воздушном слое, образованным зеркалом 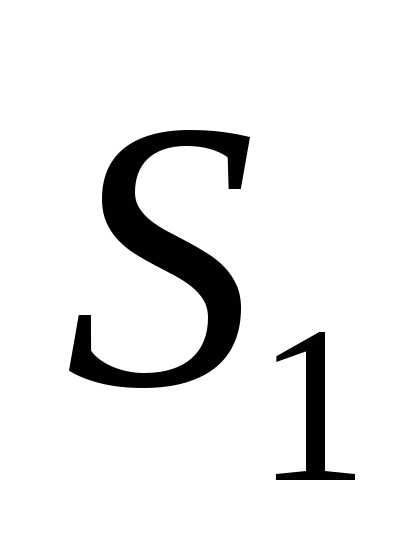 и мнимым изображением
и мнимым изображением зеркала
зеркала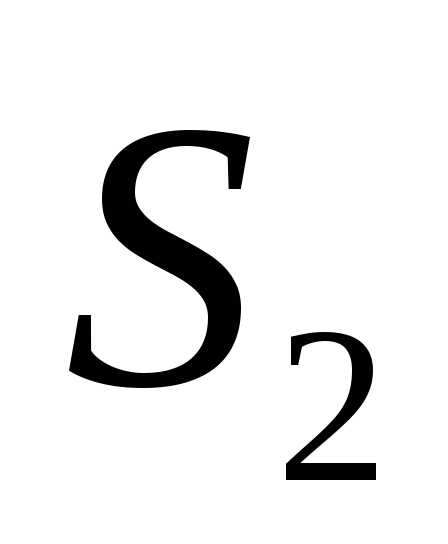 в полупрозрачной пластинке
в полупрозрачной пластинке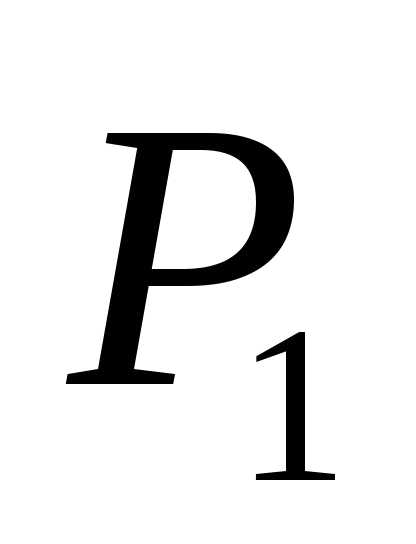 . Характер интерференционной картины зависит от положения зеркал и от расходимости пучка света, падающего на прибор. Если пучок параллелен, а плоскости
. Характер интерференционной картины зависит от положения зеркал и от расходимости пучка света, падающего на прибор. Если пучок параллелен, а плоскости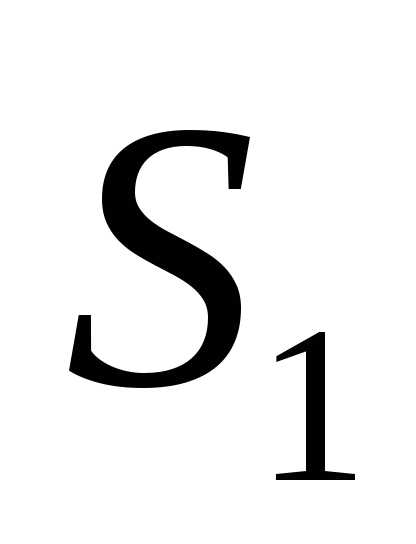 и
и образуют клин, то наблюдается интерференционные полосы равной толщины, расположенные параллельно ребру воздушного клина. При расходящемся пучке света и параллельном расположении плоскостей
образуют клин, то наблюдается интерференционные полосы равной толщины, расположенные параллельно ребру воздушного клина. При расходящемся пучке света и параллельном расположении плоскостей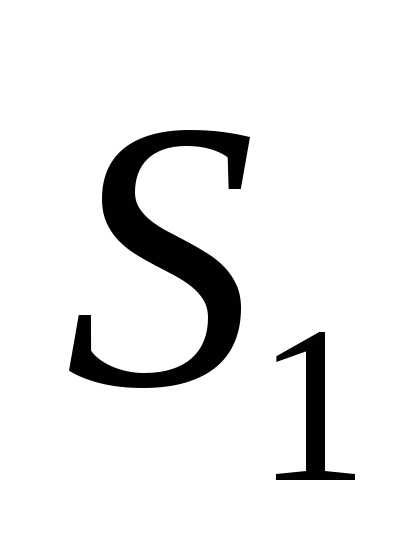 и
и получаются полосы равного наклона, имеющие вид концентрических колец.
получаются полосы равного наклона, имеющие вид концентрических колец.
Интерферометр Фабри-Перосостоит из двух параллельных стеклянных или кварцевых пластинок, разделенных воздушным промежутком (рис.). Интенсивности вышедших из прибора лучей относятся как
Соответственно отношения амплитуд будут следующими
Фаза колебания с увеличением номера луча изменяется на одну и ту же величину, определяющейся оптической разностью хода соседних лучей.
При пропускании сквозь прибор расходящегося пучка света в фокальной плоскости линзы возникают полосы равного наклона, имеющие вид концентрических колец.
Применение интерферометров весьма многообразно. Они применяются для точного (порядка 107м) измерения длин, измерения углов, определения качества оптических деталей, исследования быстропротекающих процессов и др.
studfiles.net
17.Интерференция в тонких пленках. Полосы равной толщины и равного наклона. Кольца Ньютона. Применение интерференции света.
Явление интерференции наблюдается в тонком слое несмеш-ся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек и т. д. Интерференция возникает при разделении первонач. луча света на два луча при его прохожд. через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной d , отразится дважды — от внутр. и наружной её поверхностей. Отражённые лучи будут иметь пост.разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при . Еслинм, то толщина плёнки равняется 550:4=137,5 нм.
— условие максимума;— условие минимума, где k=0,1,2… иL1,2— оптическая длина пути первого и второго луча, соответственно. Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называютсяполосами равной толщины. Кольца Ньютона.Кольца Ньютона, являющ. классич. примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образован. плоскопарал. пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона. Явление интерференции применяется для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий. Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн (интерференционная спектроскопия).
18.Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Зонная пластинка.
Дифракциейназывается огибание волнами препятствий, встреч-ся на их пути, или в более широком смысле — любое отклонение распрост-ия волн вблизи препятствий от законов геометрич. оптики. Благодаря дифракции волны могут попадать в область геометрич. тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д. Согласно принципу Гюйгенса — Френеля,световая волна, возбуждаемая каким-либо источникомS,может быть предст-а какрезультат суперпозиции когерентных вторичных волн,«излучаемых» фиктивными источниками. Такими источ-ми могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающ. источникS.Френель решил вопрос о прямолинейном распространении света, рассмотрев взаимную интерференцию вторичных волн и применив прием, получивший названиеметода зон Френеля. Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки—в простейшем случае стеклян. пластинки, состоящие из системы чередующихся прозрач.и непрозрач. концентрических колец, построенных по принципу расположения зон Френеля, т. е. с радиусамиrmзон Френеля, определяемыми выражением для заданныхзначенийа, bи(т= 0, 2,4,... для прозрачных ит= 1, 3, 5,... для непрозрачных колец).
studfiles.net
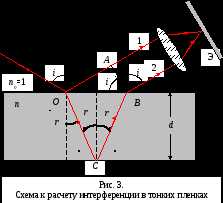
7.7. Интерференция света в тонких пленках
Многим людям приходилось наблюдать радужную окраску мыльных пленок; цвета побежалости закаленных стальных деталей, покрытых тонким прозрачным слоем окисных пленок; тонких пленок нефти, бензина, масел, плавающих на поверхности воды.
Рис. 7.11
Все эти явления вызваны интерференцией света в тонких пленках. Интерференцию света в тонких пленках можно наблюдать в проходящем или отраженном свете. Рассмотрим интерференцию света на отражение от тонкой прозрачной пленки (пластинки) толщиной d с абсолютным показателем преломления n (рис. 7.11). Пластинка (пленка) находится в вакууме (n1 = nвак = 1, - длина волны света в вакууме, причем n > n1).Пусть на пленку падает плоская монохроматическая волна под углом (луч АО). В т. О на верхней поверхности этот луч частично отражается (луч ОМ) и частично преломляется (луч ОС). Преломленный луч ОС, достигнув нижней поверхности пленки, в т. С испытывает, в свою очередь отражение (луч СЕ) и преломление (луч СN), переходя снова в вакуум.
Отраженный луч СЕ на верхней поверхности пленки в т. Е испытывает частичное отражение (луч ЕК) и частичное преломление (луч ЕР).
Преломленный луч ЕР и отраженный луч ОМ когерентны и при наложении интерферируют. Действительно, если на их пути поставить собирательную линзу, то в т. К на экране можно наблюдать интерференционную картину на отражение, максимум и минимум которой будут определяться оптической разностью хода, возникающей между лучами ОМ и ЕР от точки 0 до плоскости ЕМ, т. е.
(7.45)
где слагаемое /2 возникает из-за потери полуволны при отражении света на границе раздела вакуум-пленка в т. О.
Согласно рис. 7.11 ОС = СЕ = 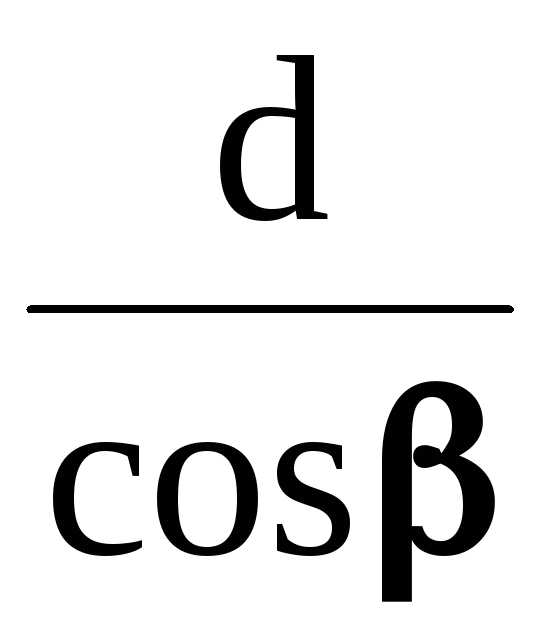 , ОМ = ОЕsin = 2dntgsin.
, ОМ = ОЕsin = 2dntgsin.
Применяя закон преломления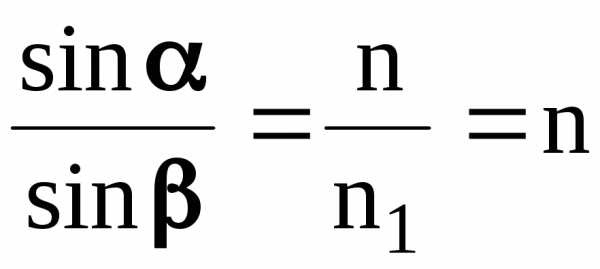 , (n1 = 1)
, (n1 = 1)
получаем после подстановки в (5.38) оптическую разность хода лучей на отражение
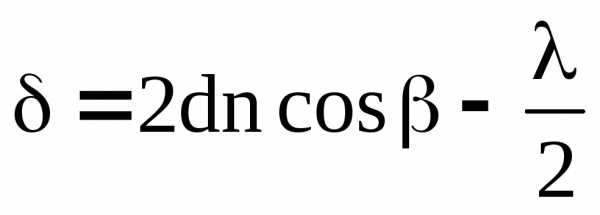 (7.46)
(7.46)
или . (7.47)
При мах = 2m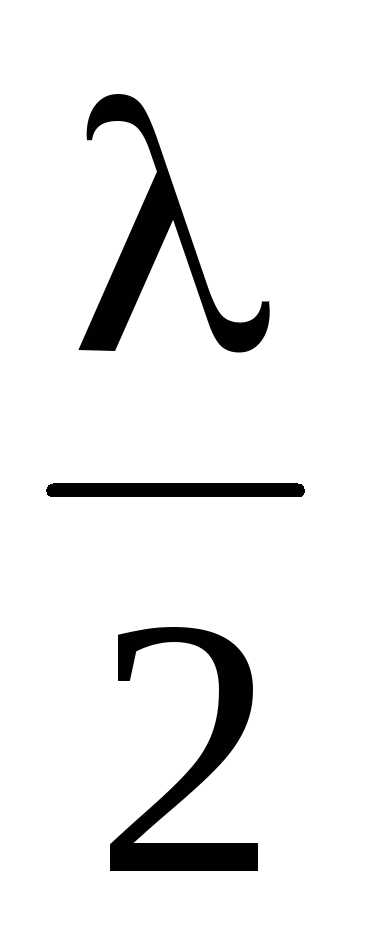 максимум интерференции в тонких пленках на отражение удовлетворяет условию . (7.48)
максимум интерференции в тонких пленках на отражение удовлетворяет условию . (7.48)
При min = (2m + 1)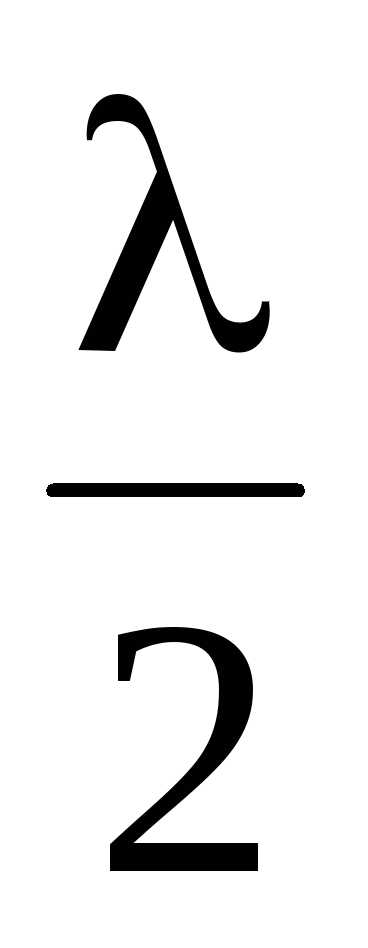 получаем условие минимума интерференции в тонких пленках на отражение, т. е.
получаем условие минимума интерференции в тонких пленках на отражение, т. е.
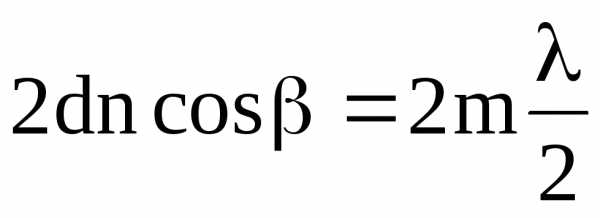 . (7.49)
. (7.49)
Аналогичный расчет можно провести для интерференции в тонких пленках на просвет в т. Q. Однако дополнительной оптической разности хода в этом случае не наблюдается. Поэтому максимум интерференции в тонких пленках на просвет соответствует условию минимума на отражение - формула (7.49) и, наоборот, минимум интерференции в тонких пленках на просвет соответствует максимуму на отражение - формула (7.48).
При освещении пленки белым светом для некоторых длин волн будет выполняться условие максимума, а для других - условие минимума, поэтому пленка в отраженном свете выглядит окрашенной.
7.8. Полосы равного наклона
При падении сходящегося (расходящегося) пучка света на плоскопараллельную пластинку (пленку) при интерференции могут возникнуть полосы равного наклона. Для каждой пары лучей 1 и 1*, 2 и 2* (рис. 7.12) оптическая разность хода определяется формулой
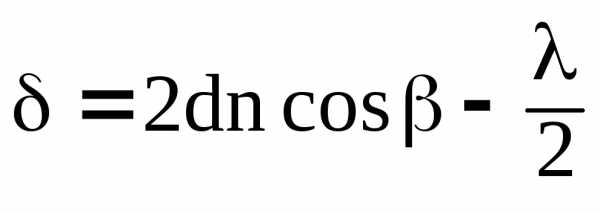 .
.
Рис. 7.12
Для каждой из пар значений - различны, так как 1 2.При наблюдении интерференционной картины используют собирательную линзу (Л) и экран (Э). В каждой точке экрана собираются и интерферируют лучи, которые после отражения от пленки параллельны прямым линиям, соединяющими их с оптическим центром линзы 0 (рис. 7.12). Например, лучи 1 и 1* - в т. В, лучи 2 и 2* - в т. А и т. д. Любая линза не создает дополнительной оптической разности хода между лучами, фокусируемыми ею на экране.
Интерференционная картина на экране имеет вид чередующихся светлых и темных полос (полосы равного наклона), каждой из которых соответствует определенное значение угла падения .
Максимум или минимум интерференции на отражение в этом случае зависти от угла падения лучей. При освещении пленки белым светом на экране возникает система разноцветных полос равного наклона.
Если оптическая ось линзы перпендикулярна поверхности пленки, то полосы равного наклона имеют вид чередующихся концентрических темных и светлых колец. В отсутствии линзы лучи 1 и 1*, 2 и 2* уходят в бесконечность.
Следовательно, полосы равного наклона локализованы в бесконечности. Это явление используется на практике для точного контроля степени параллельности тонких пленок (пластин). Изменение толщины пленки на 108 м можно обнаружить по искажению формы колец равного наклона.
studfiles.net
Интерференция света в тонких плёнках. Полосы равного наклона и равной толщины. Кольца ньютона. Практическое применение интерференции.
Интерференция света в тонких плёнках.
Интерференцию света можно наблюдать не только в лабораторных условиях с помощью специальных установок и приборов, но и в естественных условиях. Так, легко наблюдать радужную окраску мыльных пленок, тонких пленок нефти и минерального масла на поверхности воды, оксидных пленок на поверхности закаленных стальных деталей (цвета побежалости). Все эти явления обусловлены интерференцией света в тонких прозрачных пленках, возникающей в результате наложения когерентных волн, возникающих при отражении от верхней и нижней поверхностей пленки.
Оптическая разность хода лучей 1 и 2
 (6)
(6)
Где п – показатель преломления пленки; n0 – показатель преломления воздуха, n0 = 1; λ0/2 – длина полуволны, потерянной при отражении луча 1 в точке о от границы раздела с оптически более плотной средой (n >n0,).
;
;
;
.
. (7)
Полосы равного наклона и равной толщины.
Полосы равной толщины и равного наклона наблюдаются при интерференции волн, отраженных от двух границ прозрачной пленки или плоскопараллельной пластинки.
Полосы равного наклона локализованы на бесконечности.
Полосы равной толщины локализованы в плоскости, отражающей пленки. В пределах ширины пленки можно считать, что интерференционная картина локализована там, где вам удобнее.
Для наблюдения полос равной толщины отражающие поверхности не обязательно должны быть идеально плоскопараллельны. Пара отражающих плоскостей может образовывать тонкий клин. Могут быть соприкасающиеся поверхности, одна или обе из которых сферические (кольца ньютона).
Более того, две отражающих поверхности могут быть расположены в разных местах, как в интерферометре майкельсона (рис.28). Здесь s — источник света, p — экран для наблюдения интерференции отраженных волн от зеркал 1 и 2, 3 — полупрозрачная пластинка. Если зеркало 2 мысленно отразить в полупрозрачной пластинке 3, то его изображение примет положение 2'. Вместе с зеркалом 2 мысленно отобразим в полупрозрачной пластинке и все лучи, идущие справа от нее к зеркалу 2 и от него обратно к полупрозрачной пластинке. Тогда на экран p свет будет приходить, как бы отражаясь от двух плоскостей 1 и 2'. Если дополнить интерферометр двумя линзами, как это обычно делается (рис. 29), то, в зависимости от расстояния между линзой l2и экраном p, можно наблюдать полосы равной толщины (1/a1+ 1/a2= 1/f2) или полосы равного наклона (a2= f2).
Рис. 29
Рис. 28
Кольца ньютона.
К ольца ньютона представляют собой интерференционные полосы, возникающие при наложении волн, отраженных от верхней и нижней поверхностей тонкой воздушной прослойки, заключенной между стеклянной пластинкой и наложенной на нее линзой большого радиуса кривизны (рис.2).
Ширина воздушного слоя увеличивается от точки соприкосновения n к краям линзы. В точках p1 и p2, равноотстоящих от точки n, толщина слоя одинакова. На всей поверхности пластины равные толщины слоя располагаются по концентрическим окружностям с центром в точке n. Если осветить систему пластинка - линза почти параллельным пучком монохроматческого света., то в отраженном свете наблюдается большое число чередующихся светлых и темных концентрических колец с темным пятном в области точки n. Эти полосы равной толщины называются кольцами ньютона. Темное пятно в центре колец (при наблюдении в отраженном свете) объясняется тем, что геометрическая разность хода между интерферирующими волнами в области точки n практически равна нулю и лишь теряется полуволна при отражении от поверхности линзы.
Разность хода интерферирующих волн 1 и 2 D = 2d×n. Для воздушного слоя n = 1. Кроме указанной разности хода появляется дополнительная разность хода в полволны вследствие отражения луча в точке м от оптически более плотной среды:
(8)
Таким образом, полная разность хода между волнами 1 и 2 будет:
1). Для темных колец (9)
2). Для светлых колец (10)
Где m = 1,2,3…
Рассчитаем радиусы колец ньютона rm, наблюдаемых в отраженном свете.
Рис.3
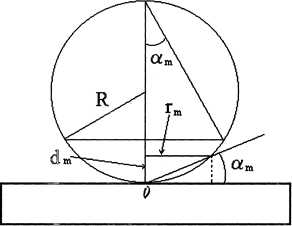
из рис.3 следует, что для кольца порядка m:
Так как dm<<2r, то 2r-dm 2r следовательно:
Откуда
(11)
Подставляя в формулы (9) и (10) выражение для dm получим:
1). Для темных колец (12)
2). Для светлых колец (13)
Из этих формул можно было бы определить l, зная радиус кольца, радиус кривизны линзы и порядок минимума (или максимума). Однако вследствие упругой деформации стекла невозможно добиться идеального соприкосновения линзы и пластинки в точке о. Поэтому более точно результат получится, если вычислять l по разности диаметров двух колец порядка dk и dm. Для темных колец имеем:
Откуда
(14)
Таким образом, зная радиус кривизны линзы и диаметры темных интерференционных колец:, можно по формуле (14) вычислить длину световой волны l.
Практическое применение интерференции.
Использование интерференции в технике. Явление интерференции света находит широкое применение в современной технике. Одним из таких применений является создание "просветленной" оптики. Отполированная поверхность стекла отражает примерно 4% падающего на нее света. Современные оптические приборы состоят из большого числа деталей, изготовленных из стекла. Проходя через каждую из этих деталей, свет ослабляется на 4%. Общие потери света в объективе фотоаппарата составляют примерно 25%, в призменном бинокле и микроскопе - 50% и т. Д.
Для уменьшения световых потерь в оптических приборах все стеклянные детали , через которые проходит свет, покрывают пленкой, показатель преломления которой меньше показателя преломления стекла. Толщина пленки равна четверти длины волны.
Другим применением явления интерференции является получение хорошо отражающих покрытий, необходимых во многих отраслях оптики. В этом случае используют тонкую пленку толщиной l/4 из материала, коэффициент преломления которого n 2 больше коэффициента преломления n 3 . В этом случае отражение от передней границы происходит с потерей полволны, так как n 1 < n 2 , а отражение от задней границы происходит без потери полволны (n 2 > n 3 ). В результате разность хода d = l/4+l/4+l/2=l и отраженные волны усиливают друг друга.
И. С. Широко используется при спектральном анализе для точного измерения расстояний и углов, в рефрактометрии, в задачах контроля кач-ва поверхностей, для создания светофильтров, зеркал, просветляющих покрытий и др.; на явлениях и. С. Основана голография. Важный случай и. С. - интерференция поляризованных лучей.
Дифракция света. Принцип Гюйгенса – Френеля. Зоны Френеля. Дифракция Френеля на малом круглом отверстии. Дифракция Фраунгофера на одной щели. Дифракция Фраунгофера на дифракционной решетке. Дисперсия и разрешающая способность дифракционной решетки.
Дифракция света.
Похожие статьи:
poznayka.org


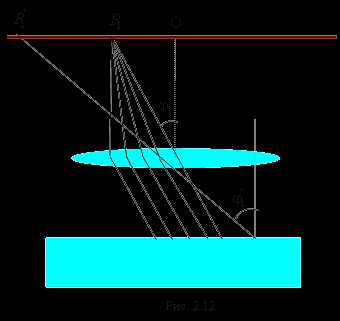 Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом. Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран (рис. 2.12). В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом , после отражения от обеих поверхностей пластинки соберутся линзой в точке и создадут в этой точке освещенность, определяемую значением оптической разности хода. Лучи, идущие в других плоскостях, но падающие на пластику под тем же углом, соберутся линзой в других точках, отстоящих от центра экрана на такое же расстояние, как и точка . Освещенность во всех этих точках будет одинакова. Таким образом, лучи, падающие на пластинку под одинаковым углом , создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром точке О. Аналогично, лучи, падающие под другим углом , создадут на экране совокупность одинаково освещенных точек, расположенных по окружности другого радиуса . Но освещенность этих точек будет иной, так как им соответствует другая оптическая разность хода.
Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом. Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран (рис. 2.12). В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом , после отражения от обеих поверхностей пластинки соберутся линзой в точке и создадут в этой точке освещенность, определяемую значением оптической разности хода. Лучи, идущие в других плоскостях, но падающие на пластику под тем же углом, соберутся линзой в других точках, отстоящих от центра экрана на такое же расстояние, как и точка . Освещенность во всех этих точках будет одинакова. Таким образом, лучи, падающие на пластинку под одинаковым углом , создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром точке О. Аналогично, лучи, падающие под другим углом , создадут на экране совокупность одинаково освещенных точек, расположенных по окружности другого радиуса . Но освещенность этих точек будет иной, так как им соответствует другая оптическая разность хода.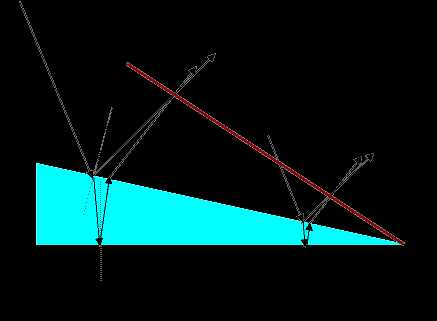 Два до падения на пластинку практически сливающихся луча после отражения от верхней и нижней поверхностей клина пересекаются в точке . Два практически сливающихся луча после отражения пересекаются в точке . Можно показать, что точки и лежат в одной плоскости, проходящей через вершину клина О.
Два до падения на пластинку практически сливающихся луча после отражения от верхней и нижней поверхностей клина пересекаются в точке . Два практически сливающихся луча после отражения пересекаются в точке . Можно показать, что точки и лежат в одной плоскости, проходящей через вершину клина О.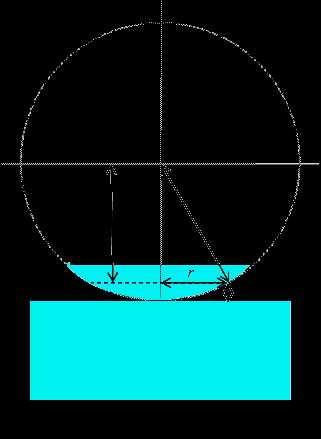 Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 2.15). Роль тонкой пленки, от поверхности которой отражаются волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид окружностей, при наклонном – эллипсов.
Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 2.15). Роль тонкой пленки, от поверхности которой отражаются волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид окружностей, при наклонном – эллипсов.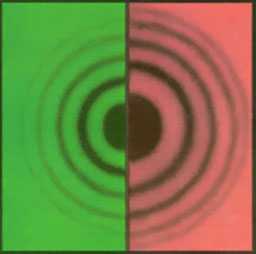 Рис. 2.16
Рис. 2.16










